Seja . Determine o que se pede, justificando adequadamente o que não há.
Domínio de .
Assíntotas horizontais e verticais da curva
Passo 1
Para o domínio de devemos lembrar que o termo dentro de um logaritmo deve sempre ser maior , enquanto o termo dentro de uma raiz quadrada deve sempre ser maior ou igual a.
Vamos analisar dentro da raiz. Lá temos a seguinte condição,
Repara que temos do somatório de e são valores sempre positivos. Ou seja, não teremos nenhuma restrição para raiz.
Seguindo o mesmo raciocínio para analisar a parte logarítmica, temos que o resultado da raiz sempre será positivo. Não havendo restrições também.
Portanto, temos que,
Passo 2
Uma vez que não existem descontinuidades no domínio não teremos assíntotas verticais.
Vamos focar nas assíntotas horizontais. Podemos pensar na assíntota como uma linha horizontal imaginaria que nunca será tocada.
Para isso, verificamos o limite em
Primeiro vamos de
Repara que ele vai para o infinito, então não temos uma linha na horizontal que não será cortada, já que a função tá sempre subindo.
Agora vamos analisar
Aqui encontramos uma assíntota horizontal em .
A gente já encontrou a assíntota, mas vamos olhar o gráfico por curiosidade,
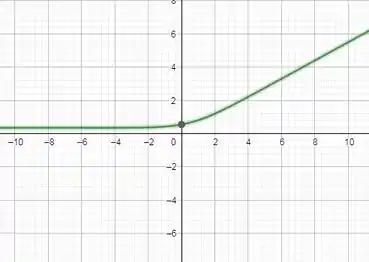
Repara que temos uma linha horizontal imaginaria quando vamos para valores de negativos.