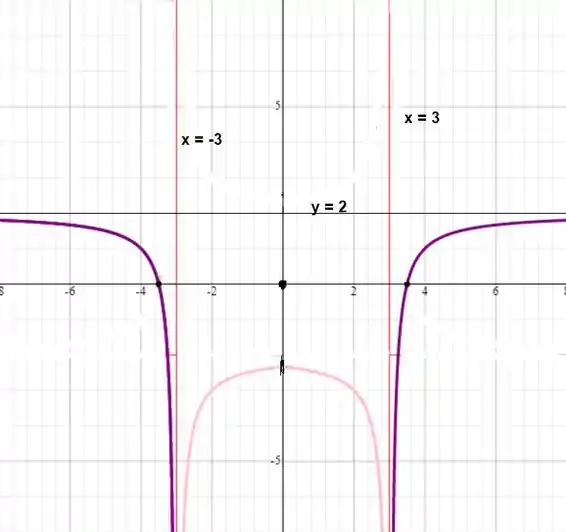
Esboce o gráfico e de um exemplo de uma função que satisfaça todas as seguintes condições dadas: , .
Passo 1
Falaaa, beleza?? Bora lá para mais um probleminha, agora o último dessa prova. Nesse exercício uma ideia é sair de uma função que faz algo que nós queremos e ir ajustando, bora lá.
Começar pela primeira condição, quando . Quando pensamos em algo indo para ela é do tipo , ou seja, queremos algo do tipo:
Mas nesse caso temos o gráfico:
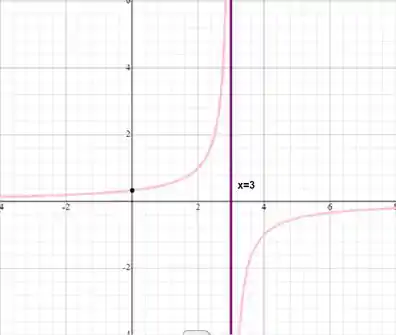
Mas veja que nesse caso, o limite para vai para pela direita e pela esquerda. Para gente fazer essa função ser par, podemos aplicar módulo em , pois vamos lembrar que é par se , ou seja, se colocarmos módulo, resolveríamos isso. Uma vez que .
Passo 2
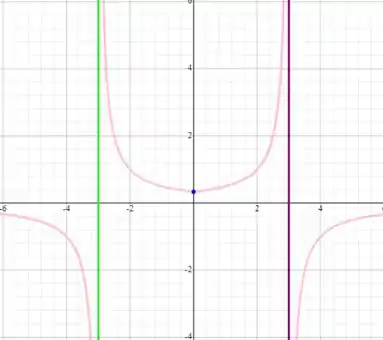
Vamos olhar para , ficaríamos com o gráfico:
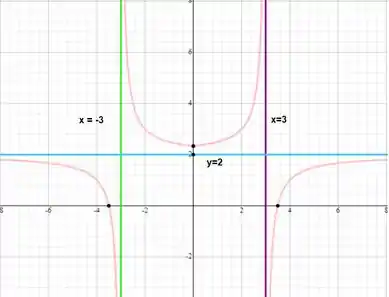
Além disso, queremos que quando , ou seja, podemos somar no valor de para subir esse gráfico 2 unidades, então
tem gráfico:
Passo 3
Nesse momento temos que as condições , falta que , porém para isso ocorrer, esse gráfico entre teria que ser para baixo, para os gráficos laterais em serem iguais, ou seja, podemos tomar:
E nesse caso, temos o gráfico sendo: