UNICAMP – Cálculo 1 – Provas Antigas – P2 – 2022.1 - 6ª Diurno – Questão 5
Seja .
- Determine os intervalos de crescimento/decrescimento de e os seus pontos de máximo/mínimo locais.
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
- Caso existam, encontre as assíntotas horizontais e verticais de .
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Passo 1
Eaeeee, belezinha??? Vamos juntos fazer devagarinho essa questão... começando pela letra (a)!!
Vamos primeiro derivar a função, desse jeitinho aqui:
Para encontrar os pontos críticos, fazemos :
ou
Assim, pelo Teste de Crescimento/Decrescimento, podemos concluir que:
E, olhando os pontos críticos percebemos que:
- muda de positivo para negativo em . Logo, é máximo local;
- muda de negativo para positivo em . Logo, é mínimo local.
Passo 2
Na letra (b) temos primeiro que calcular a derivada segunda, ou seja:
Assim, sabemos que apenas quando ou .
Além disso, podemos concluir que, quando :
- em sendo côncavo para baixo pelo Teste da Concavidade;
- em sendo côncavo para cima pelo Teste da Concavidade.
Para o ponto de inflexão (um ponto sobre uma curva na qual a curvatura muda de sinal), podemos ver que ocorre quando .
Pois logo em seguida você verá que muda de concavidade!!
Passo 3
Para a letra (c), vemos que não possui assíntota vertical pois a função é contínua em todo o .
Também, não haverá assíntotas horizontais pois:
Passo 4
Por fim, para a letra (d) podemos plotar o gráfico da função:
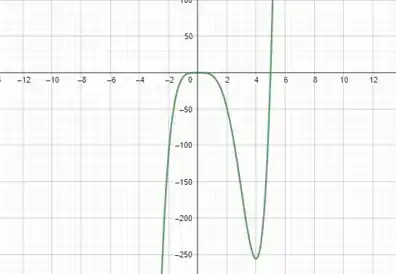
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)