Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Passo 1
Primeiro passo é a gente entender como calculamos uma assíntota vertical e uma horizontal.
De forma bem sucinta e prática:
Assíntota horizontal: Fazemos e e se , onde c é uma constante, temos uma assíntota horizontal. Lembrando que podemos ter valores de constantes dependendo se estamos fazendo e , logo teríamos 2 assíntotas horizontais nesses dois valores diferentes de constantes.
Assíntota vertical: Precisamos encontrar um valor de que faça o denominador tender a zero, se a , temos então uma assíntota vertical no valor que fizemos tender.
Então, bora pro rolo!
Passo 2
Pra gente encontrar a assíntota horizontal, vamos aplicar nosso limite!
Opa, não temos assíntota horizontal.
Passo 3
Para assíntotas verticais, precisamos lembrar que
Logo, precisamos fazer x tender a valores que zerem cos(x). Olhando pro círculo trigonométrico...
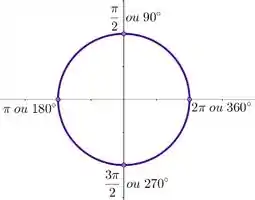
Cos(x) será zero sempre que ele for , depois , ou seja, eu precisei percorrer um tamanho do círculo pra chegar até o Depois em pra zerar cos(x) vamos precisar percorrer mais, ou seja, , e assim por diante. Note que de até eu precisei andar , ou seja, cos(x) zera toda vez que .
Logo,
Note que o numerador vai ficar variando entre – 1 ou 1 por conta do sem(x). Logo, o resultado disso vai nos dá um numerador que varia entre – 1 ou 1, e o denominador se aproxima de zero, logo o resultado desse limite ora será e ora será
Resposta
Não há assíntota horizontal
Assíntota vertical: