Determine:
As assíntotas da função
Passo 1
Falaaaa, beleza?? Bora lá para mais um probleminha dessa prova.
Esse exercício nos pede para achar assíntotas, vamos lembrar um pouco sobre esse conceito? Primeiro temos dois tipos de assíntotas as verticais e as horizontais, se lembra como acha-las?
Informalmente podemos entender assíntotas horizontais ou verticais como uma reta imaginária que delimita a aproximação de uma função no gráfico à medida que ela cresce ou decresce.
Para achar assíntotas horizontais, fazemos duas coisinhas:
Primeiro fazemos e depois , se der de fato um valor real, quando colocamos algum desses limites, dizemos que será uma assíntota horizontal. Essas retinhas são coisas do tipo:
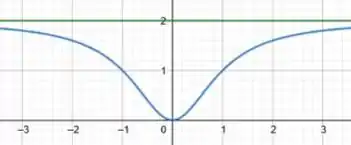
Para achar as verticais nós iremos basicamente olhar o que ocorre nos valores problemáticos no domínio da função, em geral, vamos só olhar para o valor que zera o denominador de e calcular os limites laterais nesse valor, caso algum desses resulte em acharemos uma assíntota.
Essas verticais, graficamente, são desse tipo:
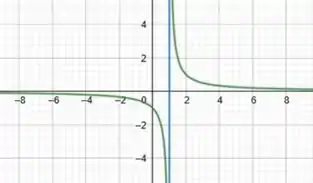
Passo 2
Agora que já demos uma revisadinha no conceito, bora para o problema.
Vamos olhar para as assíntotas horizontais, bora começar calculando:
Nesse caso, podemos analisar pelo teorema do confronto, ou seja, nossa ideia é ver o limite da seguinte forma:
Veja que nesse caso temos uma função que vai para zero vezes outra função que é limitada , ou seja, usando o teorema do confronto podemos dizer que esse limite vai para zero.
Além disso, olhando para podemos tomar a mesma conclusão, uma vez que também irá para zero.
Ou seja, temos que
E por isso achamos uma assíntota horizontal.
Passo 3
Agora vamos procurar as verticais, para isso temos que analisar os limites laterais sobre um valor problemático do domínio.
Mas veja que como o valor problemático será , pois zera o denominador, ou seja, queremos analisar:
E
Porém aqui ocorre algo legal, vamos lembrar que do limite fundamental trigonométrico, que nos diz:
Ou seja, quando temos estamos dizendo que esse limite existe e é igual a 1, ou seja, para o limite existir, os laterais devem existir e serem iguais ao limite geral, logo podemos dizer que:
Ou seja, como esses limites laterais não vão para não temos assíntotas verticais.
Assim terminamos mais um probleminha dessa prova, bora para o próximo?