UFU – Cálculo 1 – Listas – Professor Sato
7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.
c)
Passo 1
Falaaa... beleza??
Nessa questão queremos saber se a função tem assíntota vertical. Geralmente isso acontece quando a função vai pra infinito, certo? E isso acontece quando temos alguma divisão por zero.
Passo 2
A divisão por zero vai aparecer quando:
Então temos três opções de :
Passo 3
Quando , temos:
Então é assíntota vertical.
Quando , temos:
Então é assíntota vertical.
Passo 4
Quando , temos:
Como apareceu indeterminação, vamos fatorar esses polinômios:
Então não é assíntota vertical.
Para o gráfico:
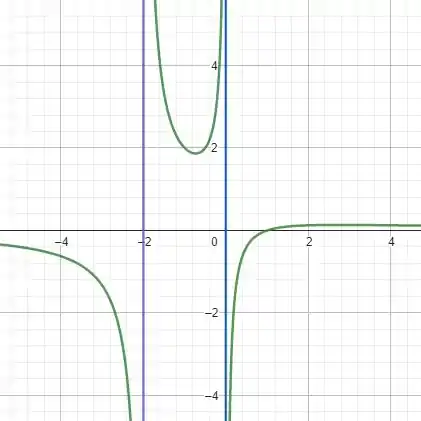
Resposta
Resposta nos passos
Exercícios de Livros Relacionados
Estime a assíntota horizontal da função f x = 3 x 3 + 500 x 2 x 3 + 500 x 2 + 100 x + 2000 através do gráfico de f para - 10 ≤ x ≤ 10 . A seguir, determine a equação da assíntota calculando o limite.
Faça um gráfico de f x = s e n x x Quantas vezes o gráfico cruza a assíntota?
Encontre as assíntotas horizontais e verticais y = 2 x 2 + x - 1 x 2 + x - 2
Encontre as assíntotas verticais da função y = x x 2 - x - 2 Confirme sua resposta da parte a fazendo o gráfico da função.
Nos exercícios de 49 a 56, encontre as assíntotas horizontal e vertical e faça um esboço do gráfico da equação 5 6 )x 2 y + 4 x y - x 2 + x + 4 y - 6 = 0