Considere a função , definida para todo com .
Determine as assíntotas verticais do gráfico de , se houver tais.
Determine as assíntotas horizontais do gráfico de , de houver tais.
Determine os intervalos de crescimento e decrescimento da função . Determine ainda os pontos de máximo e de mínimo de (se houver); especifique ainda se tais pontos são globais (absolutos) ou locais (relativos).
Determine os intervalos de concavidade para cima e para baixo do gráfico de , assim como seus pontos de inflexão (se houver).
Usando as informações obtidas nos itens anteriores, esboce o gráfico de . Deve incluir as assíntotas (se houver), e deve marcar os pontos notáveis obtidos junto com suas coordenadas.
Passo 1
Fala galerinha, nessa questão, vamos fazer um esboço do gráfico de e para isso vamos seguir o passo a passo das letras do enunciado, começando com a determinação das assíntotas.
Determine as assíntotas verticais.
Bom, sabemos que as assíntotas verticais são os pontos pertencentes ao conjuntos do números reais aonde o limite da função dá infinito ou menos infinito, isso é, são os pontos aonde a função vai pro infinito. O que queremos então é:
O valor de do limite acima é a nossa assíntota vertical, desde que
Uma boa forma de encontrar essa assíntota é olhar para a cara da função e ver se ela possui alguma descontinuidade. No nosso caso temos:
Podemos perceber que há uma descontinuidade em , pois teria uma divisão por zero que não é válida, então é uma boa alternativa para assíntota vertical.
E como vimos, esse limite vai para mais infinito, portanto é uma assíntota vertical e a função nesse ponto explode para mais infinitos pelos dois lados.
Passo 2
Determine as assíntotas horizontais
Aqui, nesse caso, queremos ver como a função se comporta quando tende a mais ou menos infinito.
E caso os valores desses limites seja algum valor real, então, esse valor é uma das assíntotas horizontais da função. Vamos olhar primeiro para
E caímos em uma indeterminação
No entanto, é uma indeterminação do tipo , então podemos aplicar L’hospital e derivar em cima e em baixo.
E bora de L’hospital de novo!
Beleza, então descobrimos que quando tende a , a função também vai para , portanto, não há assíntota horizontal para a direita. Vamos ver agora para a esquerda.
Portanto, teremos uma assíntota horizontal em e quando tende a a função tende a zero.
Passo 3
Determine os intervalos de crescimento e decrescimento. Determine os máximos e mínimos e diga se são locais ou globais.
Para avaliar o crescimento e o decrescimento da função, precisamos avaliar a sua primeira derivada, pois sabemos que se a derivada for positiva, a função cresce e se a derivada for negativa, a função decresce.
Como nossa função é , teremos aqui uma regra do quociente.
Para avaliar o sinal dessa função, podemos reparar que o termo será sempre positivo, afinal é sempre positivo para qualquer e também é sempre positivo, pois temos um expoente par.
O que altera o sinal de portanto é o termo , que pode ser aberto em
Percebemos que esse termo zera quando e quando , mas e o que acontece antes e depois desses pontos? Vamos testar alguns valores. Por exemplo, quando é menor que , vamos supor , teremos:
Então, vemos que é positiva para valores menores que e portanto também é.
E quando está entre 0 e 2, por exemplo
Daí vemos que é negativa quando está entre 0 e 2, e portanto também é.
Por fim, para valores maiores que 2, por exemplo, 2,1.
Daí vemos que é positiva e portanto é positiva para valores maiores que 2.
Sendo assim, temos o seguinte estudo de sinal da primeira derivada
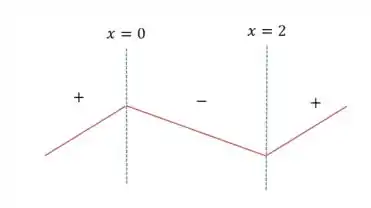
Da onde podemos reter a informação de que a função é crescente no intervalo e a função é decrescente no intervalo
Os pontos e são pontos críticos e portanto são boas opções para máximos e mínimos.
O ponto , é um ponto de assíntota vertical, pois nesse ponto a função explode para , portanto, não podemos considera-lo como um ponto de máximo, afinal esse ponto sequer está no domínio da função.
O ponto , pode ser analisado como um ponto de mínimo, pois ele passa de uma derivada negativa para uma positiva e não pertence a nenhuma assíntota. Agora para saber se ele é um mínimo local ou global, vamos avaliar o valor da função nesse ponto:
Como sabemos que a função tende a zero pela esquerda, pois uma assíntota horizontal é quando , então temos que é um ponto de mínimo local, pois a função chega em valores menores que esse.
Passo 4
Determine os intervalos de concavidade para cima e para baixo do gráfico de , assim como seus pontos de inflexão.
Determinar a concavidade tem tudo a ver com a segunda derivada, pois quando a segunda derivada é positiva, temos que a concavidade é para cima e quando a segunda derivada é negativa a concavidade é para baixo. Além disso, quando a segunda derivada é zero, temos ali um ponto de inflexão. Bora lá!
Como já derivamos a função uma vez, só basta derivar a derivada.
Mas antes, pra a gente fazer menos conta, se liga que:
Ou seja, dá pra cortar o do numerador com o denominador, é só colocar o do numerador em evidência e então cortar.
Agora sim, vamos derivar
Vou colocar o em evidência na primeira soma e deixar os em evidência em todos os termos.
Aqui podemos cortar
Agora podemos juntar os termos que estão multiplicando o
Pronto, chegamos em uma expressão para a nossa segunda derivada!
Bom, essa função vai zerar quando tende a menos infinito pois , no entanto, esse não é um ponto que devemos considerar.
Além disso, essa função também vai zerar quando for igual a zero, ou seja, temos que encontrar as raízes dessa função quadrática.
Ou seja, essa função não possui raízes reais. E como ela é contínua, ela terá sempre o mesmo sinal, vamos colocar um valor qualquer para ver qual sinal é:
Portanto, essa função quadrática é sempre positiva.
Além disso, também é sempre positiva, assim como o termo , ou seja, a segunda derivada é sempre positiva:
Portanto, a concavidade da função é sempre para cima e não há pontos de inflexão.
Passo 5
Usando as informações obtidas, esboce o gráfico de .
Agora é só juntar tudo e colocar no gráfico.
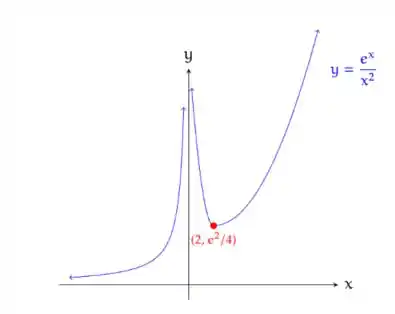
Podemos ver nesse gráfico a assíntota horizontal em e que a função tende a zero quando . Também podemos ver a assíntota vertical em e que a função explode para pelos dois lados quando .
Além disso, podemos ver que não a função vai para quando vai para , a concavidade é sempre para cima e a função cresce entre e e decresce entre .Por fim, também está apresentado em vermelho o ponto de mínimo em que é local, pois a função chega a valores menores que .
Não há pontos de inflexão.
Resposta
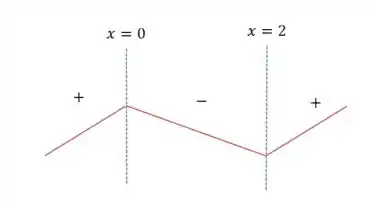
- Concavidade sempre positiva, não há inflexão.
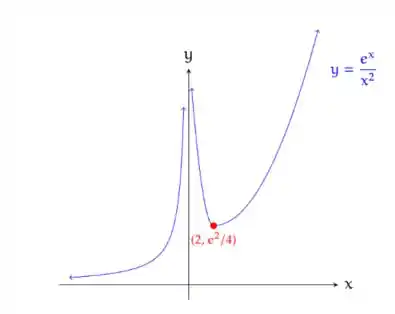
Mínimo local em