UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.7
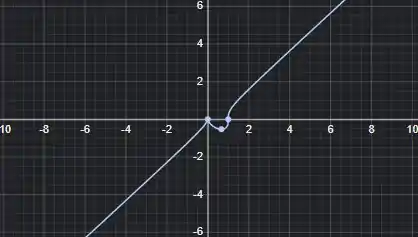
Esboce o gráfico .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar o gráfico da seguinte função:
Mas como podemos esboçar essa função???
Uma forma seria escolher valores aleatórios de e analisar os valores de correspondentes e, por fim, traçarmos um gráfico... mas isso seria muito trabalhoso, né?
Então... outra opção seria a gente selecionar os pontos de interseção com os eixos, identificar as assíntotas verticais e horizontais, e determinar o comportamento da curva em torno desses pontos e assíntotas.
Então bora lá!!
😉
Passo 2
Dessa forma, vamos começar encontrando os pontos de interseção com os eixos e :
- Interseção com o eixo (fazendo ):
- Interseção com o eixo (fazendo ):
- Para valores ;
- Para valores entre e ;
- Para valores .
e
Com isso, já sabemos que o nosso gráfico passará pelos seguintes pontos e :
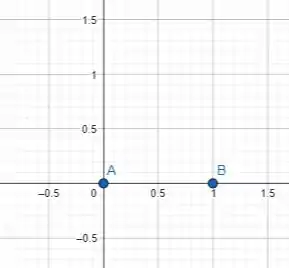
Agora temos que analisar o comportamento do gráfico nos seguintes intervalos:
Passo 3
Mas antes, vamos ver se a função tem assíntotas verticais e horizontais.
Já podemos ver, quando calculamos a interseção no eixo , que não haverá assíntotas verticais pois para e (pontos em que a função está definida e igual a zero).
Ainda, podemos ver que quando fazemos , a função também tenderá a , fazendo com que não temos assíntotas horizontais definidas.
Passo 4
Agora, vamos analisar o comportamento do gráfico para valores (ou seja, para ).
Como não há assíntotas verticais e horizontais, vamos estabelecer 3 pontos aleatórios de :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
Analisando esses valores podemos aproximar que a função tem um comportamento linear crescente para valores de .
Passo 5
Agora, vamos analisar o comportamento do gráfico para valores entre e (ou seja, para ).
Passo 6
Agora, vamos analisar o comportamento do gráfico para valores (ou seja, para ).
Analisando esses valores podemos aproximar que a função tem um comportamento linear crescente para valores de .
Passo 5
Com base nisso, podemos plotar o gráfico da seguinte forma:
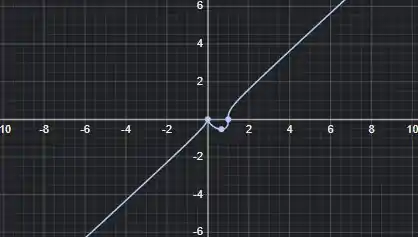
Entendeu direitinho? Responde aee ;)
Resposta
