UNICAMP – Cálculo 1 – Provas Antigas – P2 – 2022.1 - 5ª Noturno – Questão 5
Seja .
- Determine os intervalos de crescimento/decrescimento de e os seus pontos de máximo/mínimo locais.
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
- Caso existam, encontre as assíntotas horizontais e verticais de .
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Passo 1
Eaeeee, belezinha??? Vamos juntos fazer devagarinho essa questão... começando pela letra (a)!!
Vamos primeiro derivar a função, desse jeitinho aqui:
Para encontrar os pontos críticos, fazemos :
Analisando esse único ponto crítico, podemos determinar o crescimento e decrescimento da função através de cuja raiz é . Assim, temos que:
é decrescente em
E que
é crescente em
Para mais, pelo teste da derivada primeira é possível afirmar que (mínimo local que também é global por s[o ter um ponto crítico haha)
Passo 2
Na letra (b) temos primeiro que calcular a derivada segunda, ou seja:
Analisando (que tem raiz ) do produto (já que é sempre crescente), temos que:
para côncava para baixo
E que
para côncava para cima
E, os pontos de inflexão são dados pela mudança de concavidade, ou seja:
Passo 3
Para a letra (c), vemos que não possui assíntota vertical pois a função é contínua em todo o .
Logo, a assíntota horizontal é dada por:
E
Aplicando L’Hospital, temos:
Logo, a única assíntota ocorre quando .
Passo 4
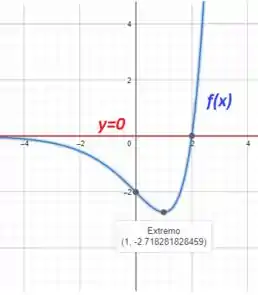
Por fim, para a letra (d) podemos plotar o gráfico da função mostrando a assíntota, o ponto mínimo, ponto de inflexão e concavidade:
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)