Encontre as assíntotas horizontais e verticais da função .
Passo 1
Beleza pessoal, pra terminar essa prova a gente tem que lembrar das definições de assíntotas horizontais e verticais.
Primeiro vamos lembrar da aparência de cada uma delas:
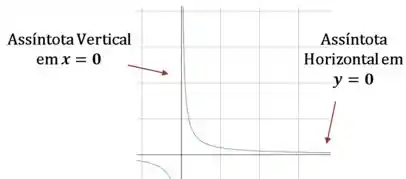
A imagem já ajuda bastante a entender as definições: a assíntota horizontal acontece nesse caso aqui:
E a assíntota vertical acontece nesse aqui:
Passo 2
Vamos começar calculando as assíntotas horizontais, que geralmente são mais fáceis de encontrar.
É só calcular o limite quando tende a mais/menos infinito. Começamos com :
Isso é o limite da divisão de dois polinômios. O que a gente pode fazer nesses casos? Uma boa tentativa é dividir tudo pela maior potência.
Nesse caso a maior potência é , então vamos dividir por em cima e embaixo:
Agora o que acontece quando tende ao infinito?
Quando fica muito grande, aquelas duas frações vão tender a zero! Então:
E o resultado vai ser exatamente o mesmo com :
Então a função tem assíntotas horizontais em :
Passo 3
Agora vamos procurar as assíntotas verticais. Esse tipo de assíntota aparece quando a função “explode” para cima ou para baixo perto de algum ponto:
Como que uma função pode explodir desse jeito? Bom, ou o numerador fica muito grande, ou o denominador fica muito pequeno.
O numerador só fica muito grande quando tende ao infinito, mas a gente já viu que isso caiu numa assíntota horizontal.
Então como a gente pode fazer pro denominador ficar muito pequeno? Fácil! É só ver qual valor de faz ele se aproximar de zero!
Passo 4
Mas pra provar mesmo que a gente tem uma assíntota nesse ponto, temos que calcular o limite:
Quando o se aproxima do pela esquerda, ele se comporta mais ou menos assim:
Ou seja, ele sempre fica abaixo do , e por isso fica sempre negativo. Por isso, quando a função explode, ela explode pra baixo.
Quando o se aproxima do pela direita, ele se comporta mais ou menos assim:
Então ele sempre fica acima do , e o vai ficar sempre positivo, e aí a função vai explodir pra cima:
Beleza, provamos que a função tem assíntotas verticais em .
Passo 5
Pra garantir que não vai sobrar dúvida, vamos fazer o gráfico da função, mostrando as assíntotas verticais em e as horizontais em :
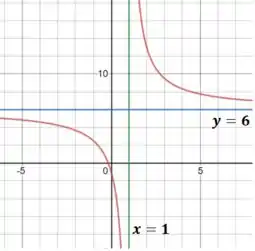
Resposta
A função tem assíntotas horizontais em , e assíntotas verticais em .