UFSC – Cálculo 1 – Lista 1.9 – Assíntotas – 21.1 – P1 – letra (j)
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Passo 1
Primeiro passo é a gente entender como calculamos uma assíntota vertical e uma horizontal.
De forma bem sucinta e prática:
Assíntota horizontal: Fazemos e e se , onde c é uma constante, temos uma assíntota horizontal. Lembrando que podemos ter valores de constantes dependendo se estamos fazendo e , logo teríamos 2 assíntotas horizontais nesses dois valores diferentes de constantes.
Assíntota vertical: Precisamos encontrar um valor de que faça o denominador tender a zero, se a , temos então uma assíntota vertical no valor que fizemos tender.
Então, bora pro rolo!
Passo 2
Precisamos lembrar de algumas coisinhas importantes aqui das funções trigonométricas. A gente sabe que a função arco tangente é a função inversa da função tangente no intervalo de . E precisamos lembrar que
E olhando pro círculo trigonométrico, temos que as assíntotas verticais de é onde fazemos tender a um valor, tal que . Para isso acontecer, podemos escrever assim então:
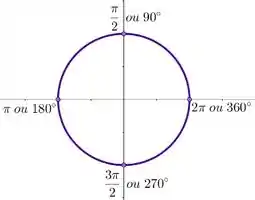
Em outras palavras, pra isso acontecer precisamos lembrar quais valores farão tender a zero para que tenda a infinito. Esses valores são e .
Passo 3
Analogamente, podemos entender que sendo a inversa de teremos uma assíntota horizontal em , pois o gráfico de uma função inversa é feita quando refletimos esse gráfico em
Ou seja, vamos pegar esse gráfico de , quando refletirmos no eixo quando , vamos ter o segundo gráfico.
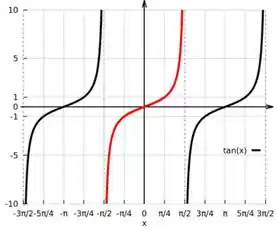
Gráfico
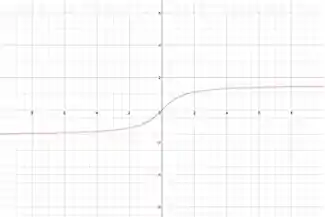
Resposta
Assíntota horizontal:
Não há assíntota vertical