- Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
k.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que determinar as assíntotas horizontais e verticais. Para quem não lembra como achá-las, é o seguinte:
- Para assíntotas horizontais: o que a gente faz aqui, basicamente, é achar o limite da função quando vai pra . Se esse valor for um número, então ali temos umas assíntota.
- Para assíntotas verticais: vamos basicamente procurar valores de que podem dar problema no domínio da função, então fazemos o limite de indo para esse ponto onde o domínio não existe. Se o limite for para infinito, temos uma assíntota vertical.
Então bora lá!
Passo 2
Vamos começar pela assíntota vertical! Para isso vamos lembrar que:
Lembrando que o denominador não pode zerar. Ou seja, são candidatos a assíntotas verticais, os pontos onde:
Como o seno zera em
Logo, teremos que calcular os limites de . Onde é um número inteiro.
Fazendo o limite:
Ou seja, temos assíntotas verticais em .
Passo 3
Para acharmos a assíntota horizontal da função cosseno, vamos fazer:
Repara que não conseguimos calcular este limite. Mas a gente pode usar uma informação sobre a função seno: ela é limitada entre e .
Ou seja, ela varia entre esses dois valores. Deste modo, podemos dizer que ela possui duas assíntotas horizontais, em:
Prontinho!
Passo 4
Uma forma de descobrir a assíntota horizontal da função cossecante é olhando o gráfico dela! Repara que a função nunca ultrapassa as linhas vermelhas:
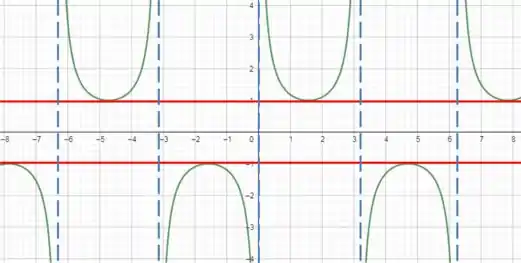
Repara que marquei de azul tracejado, as nossas assíntotas verticais!
Resposta
Assintota horizontal: e
Assuitota vertical: