UFCG, Sem Campus, Cálculo Diferencial e Integral I, 1º Estágio - 2016.1, Questão 4
Determine as assíntotas horizontais e verticais, se existir, do gráfico da função .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente determinar as assíntotas horizontais e verticais da função, que são retas das quais a curva da função se aproximam cada vez mais, sem tocá-las.
Pra determinar as assíntotas horizontais, nós vamos precisar calcular os limites:
Se esses limites existirem, teremos nossas assíntotas horizontais.
E para as assíntotas verticais, vamos olhar para os valores que poderiam dar problema no nosso domínio (os valores que não pode assumir) e calcular o limite pra quando tende a esse valor tanto pela direita quanto pela esquerda:
Se esses limites forem iguais a ou , teremos nossas assíntotas verticais.
Vamos lá!
Passo 2
Vamos começar calculando os limites de no infinito:
Vamos dividir todo mundo pela maior potência, que no caso é o :
Quando , , então:
Agora quando , temos:
Resolvendo da mesma forma, obtemos:
Então, a reta é nossa assíntota horizontal.
Passo 3
Agora vamos verificar se existem assíntotas verticais olhando para as restrições do nosso domínio. Repare que para , não pode ser igual a ou igual a , porque isso zeraria o denominador. Então, vamos usar esses valores para calcular os limites laterais:
Vamos começar calculando o limite pela esquerda:
Dividindo todo mundo por :
Vamos analisar: quando se aproxima de pela esquerda, temos , isso implica em um denominador negativo, , que se aproxima de zero. Logo,
Agora para , temos:
Quando se aproxima de pela direita, temos , isso implica em um denominador positivo, , que se aproxima de zero. Logo,
Então, temos uma assíntota vertical em .
Passo 4
Só falta a gente verificar quando . De forma semelhante ao passo , temos:
Portanto, temos uma assíntota vertical em também.
O gráfico da nossa função mostra todas as assíntotas que nós calculamos:
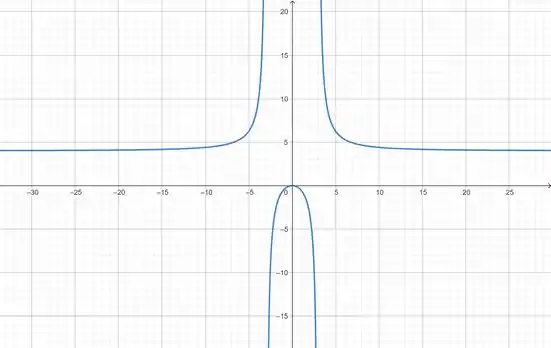
Valeu, galera! Até a próxima! 😉