Ache as assíntotas horizontais e verticais da função:
Passo 1
Olá pessoal lindo do Responde Aí, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Vamos começar?
A questão quer que encontremos as assíntotas horizontais e verticais da função
Primeiro temos que lembrar que assíntotas são linhas imaginárias que delimitam o gráfico de nossa função à medida que ele cresce ou decresce. Então temos que encontrar o valor dessas linhas para solucionar o nosso probleminha!
Para encontrar nossas assíntotas horizontais devemos calcular os seguintes limites:
e
Como nosso está tendendo ao , a dica é dividir toda a equação pelo de maior expoente para aí sim poder aplicar o nosso limite. Bora lá!
Passo 2
e
Para
É legal sempre lembramos que quando dividimos um número por outro número giganteeee como o infinito, esse número tenderá a zero. É por isso que estamos utilizando essa estratégia nessa questão. Show??
Bom sempre lembrar também que o limite de uma constante é a própria constante!
Para
Obtemos o mesmo valor, logo podemos afirmar que a assíntota horizontal é
Passo 3
Agora xuxus, para descobrirmos as assíntotas verticais temos que observar na nossa função os possíveis valores de que dariam problema em nosso domínio. Let’s go!
Sendo a nossa função
Teríamos problema em nosso domínio se o denominador desta equação for igual a zero, ou seja, se Assim,
Encontramos dois valores agora temos que conferir se os dois realmente são nossas assíntotas verticais e para isso vamos calcular o limite da nossa função tendendo a ambos os valores. Caso o nosso resultado exploda para o infinito já podemos comemorar!
Para 
Substituindo , encontramos uma indeterminação que facilmente pode ser resolvida se simplificarmos nossa expressão, fatorando o numerador e o denominador:
Logo não é nossa assíntota vertical! Vamos verificar o :
Obaaaa! O limite explodiu para o infinito, assim, o é a nossa assíntota vertical. Vamos dar uma olhadinha no gráfico para conferir se tá tudo certinho.
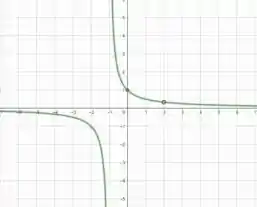
Show!!! Tudo certo 😊
Até mais!