UFRJ, Sem Campus, Cálculo 1, Listas Cálculo 1 - P2 - 2022.2, Questão 1
Considere a seguinte função e suas derivadas:
, ,
Calcule as assíntotas de , estude o sinal da primeira e segunda derivada, indique os pontos de máximo/mínimo locais, os pontos de inflexão, e faça um esboço de
Passo 1
Oiiie, tudo bem?
O enunciado nos deu uma função e suas derivadas
, ,
ele pede para calcularmos as assíntotas, o sinal da primeira e segunda derivada, obter os máximo e mínimos locais, os pontos de inflexão, e usando tudo isso, fazer um esboço! Temos bastante coisa para fazer, então vamos apresentá-las por partes! Vamos começar achando as assíntotas, e usando as derivadas dadas para calcular os pontos críticos necessários para se obter os pontos de máximo (mínimo) e inflexão! Vem comigo!
Passo 2
Assíntotas verticais estão presentes quando existem problemas no domínio de uma função, a nossa função é bem comportada para todo , portanto, não existem assíntotas verticais! Para as horizontais precisamos verificar o seguinte limite
Se é um valor finito, ele nos indicará nossas assíntotas horizontais! Primeiro, temos que
como este é um limite no infinito, e temos uma razão entre polinômios, podemos dividir o numerador e o denominador pelo termo de maior ordem dos polinômios! Ou seja, por , obtemos que
Ou seja, temos uma assíntota horizontal na reta , ela é assíntota para quando já que a nossa função tem paridade “par”. Vamos estudar o sinal das derivadas agora!
Passo 3
A nossa primeira derivada é tal que
o denominador é sempre positivo, e irrelevante para dizermos onde a derivada se anula, portanto, temos que a nossa derivada é negativa para , é positiva para , e tem o seguinte ponto crítico como , o ponto crítico é o ponto em que
Vamos usar esse ponto crítico para avaliar o sinal da segunda derivada! Saca só!
Passo 4
A segunda derivada é tal que
como temos que é sempre positivo, temos que o sinal é dado simplesmente pelo numerador, vamos encontrar quando isso é nulo, queremos verificar quando
Isolando temos que
Como temos que a segunda derivada não se anula no ponto crítico , temos que a função não tem pontos de inflexão! Será que teremos pontos de máximo ou mínimo? Vamos verificar!
Passo 5
Podemos verificar que em , nossa segunda derivada tem o seguinte valor
Portanto , indicando que este é um ponto de máximo local! E a segunda derivada é negativa em todo o intervalo
Ela é positiva em todo o resto! Como só temos um ponto crítico, esse ponto máximo local é o único que podemos encontrar, não havendo pontos de mínimo! Um esboço do gráfico deve ser parecer com
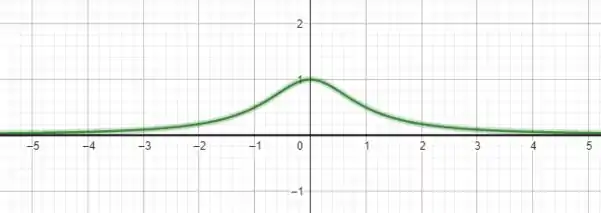
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos Passos!