Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Passo 1
Primeiro passo é a gente entender como calculamos uma assíntota vertical e uma horizontal.
De forma bem sucinta e prática:
Assíntota horizontal: Fazemos e e se , onde c é uma constante, temos uma assíntota horizontal. Lembrando que podemos ter valores de constantes dependendo se estamos fazendo e , logo teríamos 2 assíntotas horizontais nesses dois valores diferentes de constantes.
Assíntota vertical: Precisamos encontrar um valor de que faça o denominador tender a zero, se a , temos então uma assíntota vertical no valor que fizemos tender.
Então, bora pro rolo!
Passo 2
Pra gente encontrar a assíntota horizontal!!
Opa, temos indeterminações! Precisamos fazer uma mágica haha
Essa mágica é: toda vez que vermos polinômios no numerador e denominador, uma estratégia é colocar em evidência a maior potência, beleza?
Agora vamos aplicar o limite!
Concluímos que há assíntota horizontal em
Passo 3
Agora verificando a assíntota horizontal, a gente precisa determinar o valor que fará o denominador tender a zero. Como temos um polinômio, a melhor estratégia é a gente tentar encontrar as raízes do polinômio.
Passo 4
Vamos agora testar esses valores das raízes pra verificar as assíntotas verticais. Pois observe que não é porque temos duas raízes que necessariamente ambas são assíntotas verticais.
O numerador vamos ter algo positivo, certo? Uma vez que 3+ significa que estamos nos aproximando de 3 com valores maiores ele mesmo. Então nosso numerador será POSITIVO, porém será um valor muitooo próximo de zero. De igual forma, isso acontecerá também no denominador. Fazendo a análise para teremos a mesma situação, ou seja, uma indeterminação. Então, essa raiz não forma assíntota. Bora analisar a raiz
O numerador terá o valor aproximadamente de – 4, porém o denominador tenderá pra zero, ou seja, teremos .
Isso implica que em é um valor de assíntota vertical, e, graficamente temos:
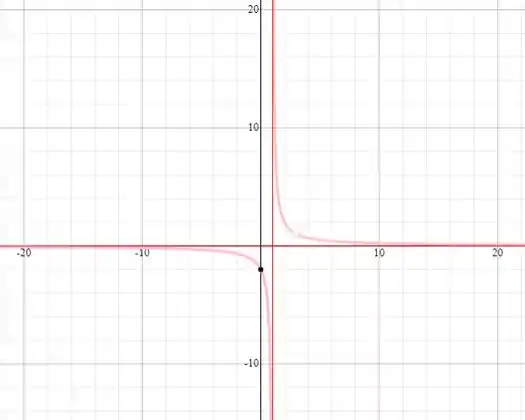
Resposta
Assíntota horizontal
Assíntota vertical