Questão 1.3 - A função terá duas assíntotas horizontais distintas se e somente se
(a) e .
(b) e .
(c) e .
(d) e .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão temos uma função que vamos chamar de dada por
Essa função deve possuir duas assíntotas horizontais e pra isso, temos que definir possíveis valores para e , no denominador da função.
Tem ideia do que fazer? 🤔
Assíntotas horizontais são retas que a função tende quando tende ao infinito, como por exemplo
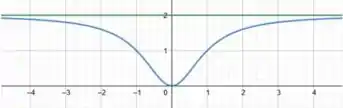
A reta verde é a assíntota e a curva azul é uma função qualquer.
Com isso, podemos dizer como obtemos uma assíntota horizontal, veja só!
Onde é uma constante onde a assíntota passa.
Entendeu? Bora começar! 😁
Passo 2
Em resumo, temos que calcular o limite de e forçar o resultado a ser uma constante. Sacou?
Começando para tendendo a
Colocando em evidência no numerador e em evidência no denominador, temos
Como , então
Assim, se , vamos obter
Vamos marcar essa etapa da resolução pois ela é muito importante!
Ta tranquilo até aqui? 👀
Passo 3
No caso, testamos fazendo tender ao infinito positivo, portanto é positivo e
Simplificando...
Substituindo por , exceto em , temos
Não ter substituído em vai nos ajudar agora, veja só!
Calculando o limite de só que dessa vez para , partindo da etapa
Agora é negativo e , logo
Substituindo por , exceto em , vamos obter
Assim, obtemos que
Agora vem o pulo do gato!
Consegue ver? 🤩
Passo 4
Foi dito no enunciado que possui duas assíntotas horizontais, portanto deve ser diferente do
Se e , então
O fato de não termos substituído em é importante, pois aqui vemos que fazendo a substituição, temos
Então vemos que a assíntota é a mesma e não é o que queremos.
O que temos que fazer então é eliminar o mal pela raiz e obrigar a ser igual a , pois assim lá no início do problema podemos desconsiderar o termo .
Já para , vemos que deve ser diferente de , pois se isso acontecer os limites e vão tender ao infinito e não teríamos assíntotas horizontais!
Assim, as assíntotas são
Analisando as alternativas, vemos que a letra c) é justamente o que acabamos de descobrir e .
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
(c) e .