UNICAMP – Cálculo 1 – Provas Antigas – P1 – 2022.1 - 6ª Diurno – Questão 4
Calcule as assíntotas horizontais e verticais da função abaixo, se existirem. Caso não existam, justifique sua resposta.
Passo 1
Eaeeee, belezinha???
Para as assíntotas horizontais, temos que verificar o limite quando e quando . Assim, vamos devagarinho aqui.
Para :
Podemos simplificar a expressão da seguinte forma:
Assim, temos o limite:
Agora vamos descobrir a outra!!
Passo 2
Para :
Podemos perceber que, para , o resultado será o mesmo de quando , ou seja:
Agora vamos descobrir as assíntotas verticais!!
Passo 3
Para se ter uma assíntota vertical em , algum dos limites laterais de em precisa ser ou .
E, para nossa função, os pontos em que isso pode ocorrer são aqueles que zeram o denominador de , ou seja, e .
Dessa forma, aplicando os limites laterais em , temos:
E
Assim, podemos que em haverá uma assíntota vertical de .
Passo 4
Por outro lado, para , temos:
E
Assim, podemos que em haverá uma assíntota vertical de .
Graficamente, temos:
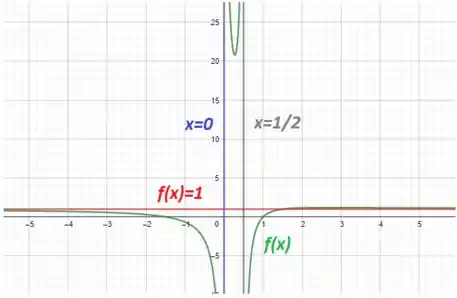
Entendeu direitinho? Responde aee ;)
Resposta
Assíntota horizontal em
Assíntotas verticais em e em