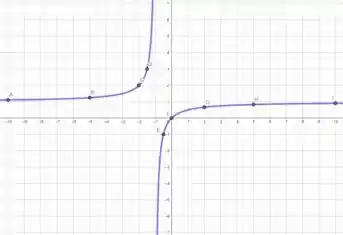
6) Esboce o gráfico de .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

A ideia por trás dessa questão é bem simples.
Foi dada uma função e precisamos esboçar o seu gráfico.
Parece tranquilo? 😁
Perceba que quando a função não está definida já que o seu denominador vai pra . Dessa forma podemos calcular os valores da imagem de alguns pontos e uni-los para esboçar o gráfico.
Entendeu? Bora lá! 😎
Passo 2
A ideia é estimar alguns valores para , substituir na função e verificar o valor que a função resulta...
Como em vimos que a função é indefinida, então vamos analisar as proximidades desse ponto depois.
Começando pelos pontos , , , e
Substituindo cada um em ...

Agora vamos ver como a função se comporta para valores abaixo de .
Por exemplo em , , e .

Entendeu essa parte? 👍
Passo 3
Agora vamos analisar a região infinitesimalmente próximo de .
Se simplesmente substituirmos por em , vamos obter
Como sabemos, não podemos dividir por , então vamos encontrar uma maneira de aproximar a imagem da função nesse ponto.
Pra isso, podemos usar o limite da função, não é? O que o limite de uma função nos resulta?
Quando calculamos o limite de uma função, estamos calculando o valor que a função tende a assumir em um ponto de análise...
Usando as aproximações em , qual é o nosso limite quando tende a a esquerda (valores infinitesimalmente menores que )?
O numerador vai tender a e o denominador vai tender a mas com valores negativos.
Por exemplo em
Perceba como o numerador é muito maior que o denominador, o que faz com que o resultado aumente com uma grande velocidade. No exemplo de , a função tende a , ou seja, se continuarmos a nossa aproximação vamos ver que tende ao infinito quando se aproxima de pela esquerda! Logo
Como em a função era já em um intervalo muito curto de valores próximos a pela esquerda vemos que a função cresceu muito rapidamente, podemos dizer que a função tende ao infinito.
Tranquilo até aqui? 👀
Passo 4
Mas e pra valores infinitesimalmente maiores que , será que o comportamento é o mesmo?
Fazendo tendendo a pela direita, por exemplo , temos
Perceba que agora a função assume grandes valores, mas negativos. Então podemos dizer que
Se em a função assumia valor e em valores próximos a pela direita a função já assumiu um valor muito baixo, então podemos dizer que a função tende a pela direita.
Agora que já sabemos seu comportamento ao longo de inclusive em , podemos esboçar seu gráfico.
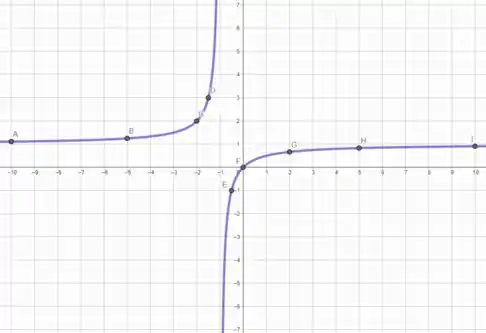
Bonitinho, não é? 🤩
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta