UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Prof° Ricardo Martins - Listas sobre Limites e Continuidade, Questão 2.10
Dê exemplos de funções com assíntotas (dois exemplos para cada tipo).
Passo 1
Eaew, beleza?
Existem três tipos de assíntotas que podem existir! Assíntotas verticais, que são caracterizadas pelo limite
no entanto, o ponto , está relacionado a valores específicos em que a nossa função não é bem definida, Temos também as assíntotas horizontais, caracterizadas por
estas são casos particulares das assíntotas oblíquas definidas por uma equação de reta da forma , em que temos
e
Vou apresentar alguns exemplos! Saca só!
Passo 2
Assíntotas verticais são funções que apresentam um ponto específico em que a função não é bem definidas, exemplos seriam funções como
e
a primeira não é bem definida em e a segunda em , ambas são assíntotas verticais! Para não nos prolongarmos muito verificando, vamos dar uma olhada nos gráficos
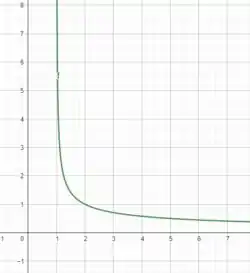
Consegue ver as assíntotas verticais em e ? Agora vamos avaliar as assíntotas oblíquas!
Passo 3
Em particular, sempre obteremos uma assíntota oblíqua quando tivermos uma razão de polinômios da forma
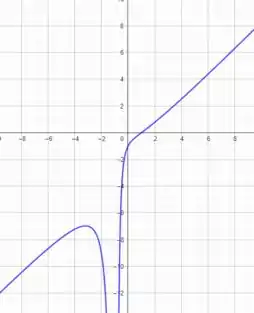
ou seja, o polinômio do numerador é exatamente um grau maior que o do denominador! Um exemplo é o seguinte
o gráfico é da seguinte forma
Um outro exemplo clássico de assíntotas oblíquas são as funções que envolvem radicais, tais como
que tem duas assíntotas oblíquas, mas se subtrairmos um , obtemos também uma assíntota horizontal
os gráficos são da forma
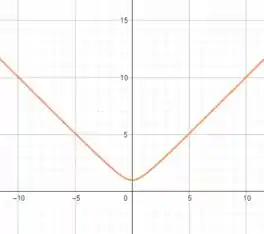
Acho que é o suficiente! Certo? A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!