Considere um sólido com base circular de raio . As secções transversais paralelas, perpendiculares à base são triangulares. Triângulos estes, isósceles com medidas de base e altura iguais. Encontre o volume deste sólido.
Passo 1
Para fazermos esse volume vamos tentar achar uma equação para essas áreas transversais, vamos dar uma interpretada gostosa no enunciado primeiro.
Ele disse que a base é um círculo de raio , a equação da base vai ser
A parte confusa a vera aqui é essa história de secções transversais paralelas, perpendiculares à base. Isso nada mais é que se cortarmos a base, perpendicularmente esse sólido, vamos encontrar triângulos isósceles.
A ideia é mais ou menos assim
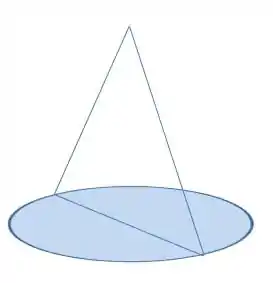
Aqui cortamos em um qualquer. Se cortarmos em um , mantendo paralelo ao eixo a base vai ser , meio louco isso né? Vamos olhar para a circunferência.
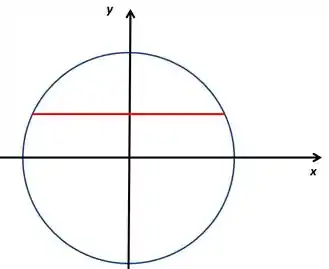
Essa linha vermelha é a base do triângulo que ele disse. Para cada valor de vamos ter uma área diferente, então podemos perceber que
Mas a área do triângulo é base vezes altura sobre , como a base e altura são iguais vamos ter
Mas queremos uma função de , então vamos usar a equação da circunferência da base que relaciona e
O valor de vai da parte de baixo da circunferência até a parte de cima, ou seja, vai de até
Passo 2
Agora vamos fazer a integral do volume, temos a fórmula da área da secção transversal, e seu limites, a integral vai ser