Calcule a integral
Onde é o conjunto
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Temos um volume para calcular, limitado por apenas duas equações, isto é:
E:
Como é a forma do nosso volume? Veja:
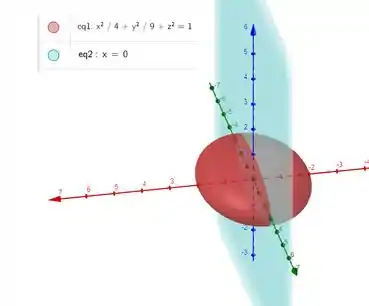
Se parece com uma elipse, certo?
Então como que calculamos? Bom, primeiramente temos que ver como são os limites de integração, e depois apenas resolver a integral! Facil, né? Vamos lá
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Temos então as equações:
E somente com essa equação podemos fazer a mágica. Como? Que por ela vamos achar os nossos limites de integração. Assim, como temos somente duas equações podemos fazer diversas ordens de integração, mas nelas devemos ter a variável por últimos, por que? Porque está definido como . Assim podemos fazer ou , como preferir, eu vou fazer , mas é porque eu quero, se fizer da outra forma vai chegar no mesmo resultado, tente veja!
Assim, de:
Isolando :
Assim:
Uma vez isolado , agora vamso isolar e achar os limites de (como já achamos os valores de integração de , vamos tomar )
Assim:
E uma vez definidos e , vamos definir (tomando )
Logo:
Mas se lembra da segunda equação que era , assim:
E definimos nossos três limites de integração. Resumindo:
E agora sim podemos fazer nossa integral
Passo 3
Sendo ela:
E agora vamos calcular esse monstrinho.
Integrando em :
Que nos resulta então em:
E como vamos resolver essa integral mostrinha.
Passo 4
Integrais desse tipo costumam ser resolvidas por uma substituição trigonométrica do tipo:
Nós temos algo do tipo , então qual seria melhor? Seria a primeira com seno e cosseno, certo? Porque podemos fazer e então . Bom, então temos:
E da derivada então:
MAS, CALMA, JOVEM MANCEBO! Atente-se, quando nós fazemos alguma substituição, qualquer que seja, nós temos que ver como que os limites de integração estão nessa substituição, assim:
Assim a nossa integral fica:
Como é constante para :
Integrando em :
Sabendo que a soma das integrais é integral da soma, podemos fazer:
E podemos então fazer as integrais separadamente, logo:
Para a primeira :
Integrando em , temos:
Para a segunda :
Integrando em :
Então agora que já temos o resultado de ambas podemos ver que:
E aqui acabamos a nossa questão, meu chapa, a resposta é . Resumindo então:
Onde é o conjunto:
Nos dá:
Obrigado por ter vindo até aqui comigo. Até a próxima.
Resposta
Onde é o conjunto:
Nos dá: