Dexter estava tomando sorvete quando de repente sentiu uma vontade enorme de saber o volume da casquinha. Tendo ela de altura e sendo composta por dois cone, um exterior com de raio e outro interior com de raio inscrito ao primeiro, ache o volume pro Dexter enquanto ele come.

Dica: o interior do cone menor é oco
Passo 1
O primeiro passo é colocar em 3D essa brincadeira pra entender melhor:
Ok, tá, isso não ajuda muito. Talvez com eixos fique melhor:
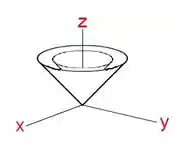
Beleza, já que o interior do cone menor é oco, a gente pode entender o volume da casquinha como o volume do cone maior menos o volume do cone menor. Vamos ter então:
Passo 2
Bem, como são dois cones, vamos primeiro fazer de forma literal e depois trocar os valores, ok? Note o seguinte, se fizermos cortes transversais perpendiculares ao eixo , acharemos sempre fatias circulares. Saca só essa fatia feito em determinada altura :
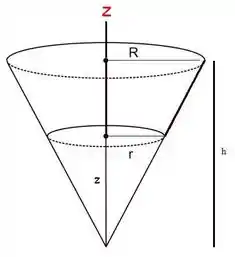
Como as fatias são circulares, a gente tem uma área dada por:
E somando os infinitos círculos que existem dentro desse cone pra diferentes alturas que possamos escolher pra fazer a fatia, temos:
Alguma simplificação a gente já consegue de cara fazer. Veja só, a pontinha do cone está na origem e o cone acaba exatamente numa altura igual sua própria altura . Pô, então sabemos os limites de integração:
E saca só, como fatias em alturas diferentes dão círculos com áreas diferentes, temos então:
Pra fechar com chave de ouro então, falta só modelar . Bora lá!
Passo 3
Nesse passo, vamos olhar de novo a mesma figura com mais calma:
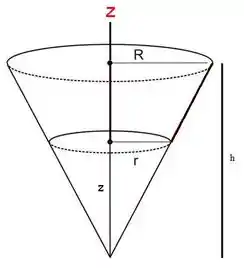
Opa, temos dois triângulos semelhantes ai em! Fazendo semelhança de triângulos, tiramos:
E logo:
O volume fica:
No final das contas, vamos ter:
Passo 4
Agora que achamos o volume de um cone de forma literal, como temos dois cones, basta aplicar! Pro cone maior, o raio era e a altura era . Logo:
E o cone menor tem a mesma altura em! O que muda é o raio que é de . Seu volume vai ser:
E finalmente podemos dizer pro Dexter o volume do cone, que vai ser: