Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volume pelas Seções Transversais

Ver Teoria
Exercício 251234567891011121314151617181920212223242627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UNICAMP – Cálculo 1 – Listas de Integrais – Questão 7.4

Encontre o volume do solido obtido pela rotação em torno do eixo y da região entre as curvas y = 4 x - x 2 e y = x . Esboce o solido e a região

Passo 1

Oi pessoal, tudo bem? Vamos começar?

O problema começa nos dando essa curva

y = 4 x - x 2

y = x

E pediu o volume do sólido formado pela rotação dela em torno do eixo y

Pergunta de milhões: Como achar esse volume?

O volume de rotação em torno do eixo x é

V = π   ∫ a b f y 2 - g y 2 d y  

Onde f é a função que está mais à direita e g a mais à esquerda. E a , b são os limites de integração do sólido. Ou onde as curvas se encontram!

Belê?

A ideia é fazer um esboço, ver os limites, tascar na fórmula e calcular a integral!

Então é isso que vamos fazer!

Mas relaxa, vou fazer passo a passo com você!

Passo 2

As curvas são

y = 4 x - x 2

→ - x 2 - 4 x + 4 + 4 = y → x - 2 2 = 4 - y

x = 4 - y + 2

x = y

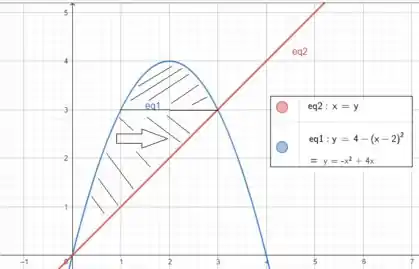Um esboço fica assim

Precisamos separar nossa integral em duas:

0 < y < 3

E o integrando

y 2 - 4 - y + 2 2 = y 2 - 4 - y + 4 + 4 4 - y

= y 2 + y + 8 + 4 4 - y

E também

3 < y < 4

E o integrando

4 - y + 2 2 - - 4 - y + 2 2 = y + 8 + 4 4 - y - 8 - y - 4 4 - y

= 2 y + 8 4 - y

Beleza?

Assim nossas integrais são

π ∫ 0 3 y 2 + y + 8 + 4 4 - y d y + π ∫ 3 4 2 y + 8 4 - y d y

Agora nossa missão é resolver a integral!

Passo 3

Calculando o volume temos

V = π ∫ 0 3 y 2 + y + 8 + 4 4 - y d y + π ∫ 3 4 2 y + 8 4 - y d y

V = π y 3 3 + y 2 2 + 8 y - 8 3 4 - y 3 2 0 3 + y 2 - 16 3 4 - y 3 2 3 4

= π 9 + 9 2 + 24 - 8 3 - - 8 3 . 8 + π 16 - 9 - 16 3

Simplificando temos

= π 64 + 9 2

E por fim

= 137 2 π

Beleza? Espero ter ajudado!

Até a próxima!

Resposta

137 2 π

Exercícios de Livros Relacionados

58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d