UFMG, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFMG - Lista 1 - Integrais Duplas e Triplas, Questão 15
Calcule o volume do sólido limitado pelas superfícies e .
Passo 1
Eaew, belezinha?
O enunciado pede para calcularmos o volume delimitado pelas superfícies
e
para isso vamos ter que calcular a seguinte integração
em que delimita a nossa região! Vamos tentar visualizá-la e encontrar os limites de integração!
Passo 2
A região é dada por
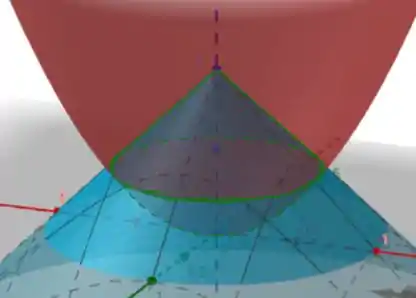
limitada superiormente pelo cone e inferiormente pelo parabolóide . Esse sólido tem uma simetria cilíndrica, então por simplicidade, vamos usar as coordenadas cilíndricas da forma
de forma que nossas superfícies possam ser escritas como e . O elemento de volume nestas coordenadas é dado por . Vamos usar tudo isso, para escrever a nossa integral! Saca só!
Passo 3
A integral de volume tomará então o formato
note que estou integrando primeiro na coordenada desde o parabolóide até o cone, e também que devido a simetria do problema, temos que o ângulo polar está dentro do intervalo a . Mas, ainda precisamos determinar o limite de integração para . Como a origem pertence a nossa região, temos que o raio inicial é , o raio final pode ser obtido fazendo a interseção das duas superfícies
que resulta na seguinte equação de segundo grau
usando Bhaskara, obtemos as raízes
pela definição da coordenada radial em coordenadas cilíndricas vamos usar a raíz positiva, desta forma, a nossa integração se torna
Vamos começar as integrações agora! Bora lá!
Passo 4
Integrando primeiramente em , temos que
Portanto, a integral de volume se torna
distribuindo o , temos que
Vamos continuar no próximo passo com as próximas integrações!
Passo 5
Para realizar as integrações em , vamos separar a nossa integral em três, da seguinte maneira
todas as integrais em podem ser resolvidas usando a fórmula
portanto, obtemos três resultados
Ou seja, nossa integral de volume se torna
A integral em é bastante direta, temos que
Ou seja, o nosso trabalho é simplificar o seguinte resultado
Bora lá!
Passo 6
Vamos primeiro evidenciar , para obter
como temos que
podemos escrever que
Fazendo um MMC, temos que
Fazendo agora o produto
de forma que temos finalmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!