Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volume pelas Seções Transversais

Ver Teoria
Exercício 911234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909293949596979899100

Enunciado

UNICAMP, Sem Campus, Cálculo 2, Atividades Profº Plínio Santini - Atividade 2, Questão 5

Determine o volume que está simultaneamente dentro das esferas

x 2 + y 2 + z 2 = 1 e x 2 + y 2 + ( z - 1 ) 2 = 1

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Cálc 2. Nosso objetivo é calcular o volume que está simultaneamente dentro das esferas.

x 2 + y 2 + z 2 = 1 e x 2 + y 2 + ( z - 1 ) 2 = 1

Passo 2

Vamos começar desenhando nosso domínio para entendermos melhor o que está acontecendo

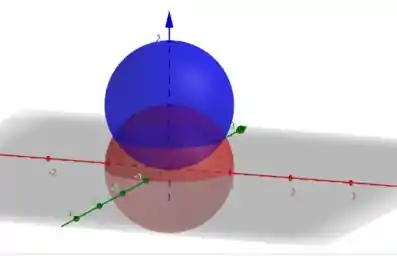
Ao analisarmos as nossas figuras, temos que a região de interesse vai da base da esfera azul, até o topo da esfera vermelha. E a projeção dessa região no plano x y é uma circunferência. Mas que circunferência é essa? Vamos descobrir. Para isso, queremos descobrir quais os valores de x   e   y que satisfazem as duas equações.

x 2 + y 2 + z 2 = 1 e x 2 + y 2 + ( z - 1 ) 2 = 1

Bem da primeira temos que

x 2 + y 2 = 1 - z 2

Substituindo na segunda equação,

x 2 + y 2 + ( z - 1 ) 2 = 1

1 - z 2 + ( z - 1 ) 2 = 1

⇒ - 2 z + 1 = 0

Logo

z = 1 / 2

Ou seja, descobrimos que o valor de z = 1 / 2 é onde ocorre a interseção das duas esferas. Logo, a projeção dessa interseção no eixo x y é:

x 2 + y 2 + z 2 = 1

⇒ x 2 + y 2 + 1 / 4 = 1

⇒ x 2 + y 2 = 3 / 4

Logo, a nossa projeção é uma circunferência.

Passo 3

Agora que temos a nossa projeção, vamos montar a integral. Mas antes disso, note que existe uma simetria na figura, então vamos particionar nosso domínio em metades. E vamos calcular a integral de uma delas. Vamos calcular a integral da metade de cima, Então queremos:

∫ 0 3 / 4 ∫ - 3 / 4 - y 2 3 / 4 - y 2 ∫ 1 / 2 1 - x 2 - y 2 d z d x d y

Mas esse domínio está horrível. Vamos fazer a nossa mudança de base e escrever em coordenadas polares. A mudança é

x = r c o s ( θ )

y = r s i n ( θ )

z = z

Fazendo o determinante da hessiana, temos que

d x d y = r d r d θ

Logo, nossa integral fica.

∫ 0 3 / 4 ∫ 0 2 π ∫ 1 / 2 1 - 3 / 4 r d z d θ d r

= ∫ 0 3 / 4 ∫ 0 2 π ∫ 1 / 2 1 - r 2 r d z d θ d r

= ∫ 0 3 / 4 ∫ 0 2 π 1 - r 2 r d θ d r - 1 2 ∫ 0 3 / 4 ∫ 0 2 π r d θ d r

Integrando temos:

= ∫ 0 3 / 4 2 π 1 - r 2 r d r - π ∫ 0 3 / 4 r d r

Por fim, usando a transformação 1 - r 2 = u ⇒ 2 r d r = - d u temos:

= - π 2 3 ( 1 - r 2 ) 3 / 2   - π r 2 2 | r = 3 / 4 r = 0

Aplicando os limites de integração

= - π 2 3 ( 1 - 3 / 4 ) 3 / 2   - π 3 / 4 2 + π 2 3

= - π 2 3 * 1 8 - π 3 8 + π 2 3

= π 2 3 * 7 8 - π 3 8

Simplificando

= 5 π / 24

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

= 5 π / 24

Exercícios de Livros Relacionados

58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d