UFSC, Joinville, Cálculo II, Provas Profº Rómulo Castillo - P2 2016.2, Questão 5b
Considere o sólido delimitada pelas superfícies Faça um esboço do sólido, mostre a região de integração e
- Formule (mas não resolva) uma integral dupla para calcular o volume do sólido.
- Formule (mas n ̃ao resolva) uma integral tripla para calcular o volume do sólido.
Passo 1
Oiee boa noite
Para visualizar e descrever o sólido T delimitado pelas superfícies , primeiro vamos esboçar o sólido e identificar a região de integração.
Esboço do sólido T:
1. A superfície define um plano inclinado que se inclina para baixo à medida que y aumenta e se estende infinitamente em x e z.
2. A superfície define outro plano horizontal paralelo ao plano xy a uma altura .
3. A curva é uma parábola que se abre para cima no plano xy e está limitada acima por que é uma linha horizontal.
Agora, vamos desenhar essas superfícies em um gráfico 3D para obter uma ideia melhor do sólido T.
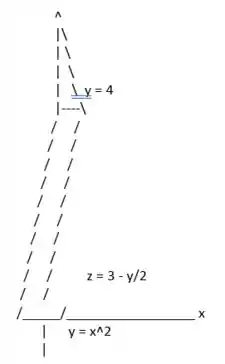
Passo 2
A região de integração é o espaço limitado pelas superfícies .
Essa região se estende infinitamente ao longo do eixo x e do eixo z, mas está limitada nos eixos y por
Portanto, a região de integração é um sólido limitado por essas superfícies.
Formulação da integral tripla para calcular o volume:
O volume do sólido T pode ser calculado usando uma integral tripla sobre a região de integração.
A integral tripla é definida da seguinte forma:
onde dV é um elemento de volume infinitesimal dentro do sólido T.
A integral tripla será sobre as variáveis , e as limitações das variáveis são as superfícies que definem o sólido.
Para definir a integral tripla, primeiro escolhemos uma ordem de integração adequada.
Vamos escolher a ordem de integração , que é a ordem mais apropriada para este sólido.
Passo 3
Então, as limitações para as variáveis são as seguintes:
- Para z: de
- Para y: de
- Para x: de algum ponto inicial até algum ponto final no eixo x (essa parte requer a determinação dos limites de integração em x).
Agora, formulamos a integral tripla:
Você precisará encontrar os limites de integração em x, que dependem da interseção das superfícies
Resolvendo , você encontrará os valores de x que definem os limites de integração em x.
Depois de encontrar esses limites, você poderá resolver a integral tripla para calcular o volume do sólido T.
Resposta
Vide a explicação.