UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Pedro Hinojosa - Lista de Exercícios 3, Questão 2d
Calcule o volume obtido ao girar a região limitada pelas curvas dadas em torno do eixo :
d) , . ;
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume de rotação da região da curva em torno do da reta , que é paralea ao eixo . Ele fala também que a região de interesse vai de a . Sendo assim, nossa região em amarelo, vai rotacionar em torno da reta em verde na figura:
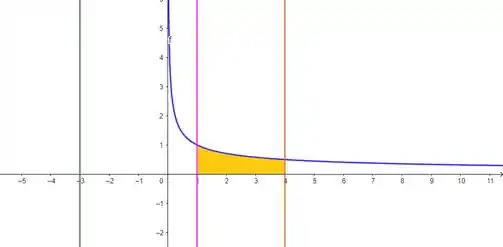
Pra calcular o volume desse sólido pela revolução da região em torno do eixo paralelo a , vamos usar o método das cascas cilíndricas, porque seria mais complicado usar o método do anel. Então, nossa integral de volume vai ter essa cara:
No nosso caso, o raio da casca é dado pela distância da reta de rotação até a função, temos:
A altura vai ser a própria função
O intervalo de integração vai da reta a . Assim, vamos montar nossa integral e calcular o volume de rotação.
Vamos lá!
Passo 2
Montando a integral, temos:
Multiplicando termo a termo:
Integrando cada termo, usando a regrinha da potência (), temos:
Aplicando os intervalos de integração:
Prontinho, galera! Até a próxima! 😉