Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volume pelas Seções Transversais

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 15

Fez-se um orifício circular em uma esfera, de forma que o eixo do orifício coincidiu com o diâmetro da esfera. Calculou-se o volume do sólido restante e obteve-se

V = 2 ∫ 0 2 π ∫ 1 2 ∫ 0 4 - r ² r d z d r d θ

Determine o raio do orifício, o raio da esfera e o Valor de V .

Passo 1

Fala aí galera, bora resolver o nosso exercício? Vamos pegar aqui a nossa integral tripla:

V = 2 ∫ 0 2 π ∫ 1 2 ∫ 0 4 - r ² r d z d r d θ

Por meio dessa integral, a gente vai conseguir interpretar o que está acontecendo e calcular tudo o que é pedido.

Para começar, vamos colocar aqui um esboço genérico do que cada coordenada ali representa:

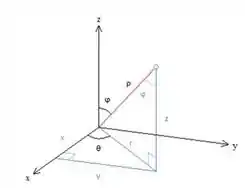
Passo 2

Para começar, vamos identificar o valor de cada raio pedido

V = 2 ∫ 0 2 π ∫ 1 2 ∫ 0 4 - r ² r d z d r d θ

Reparem que pela integral, o raio é a integral do meio, aonde o intervalo de integração:

1 ≤ r ≤ 2

No caso de uma esfera normal, o raio deveria variar da origem até o final, ou seja, nesse caso seria sem o orifício:

0 ≤ r ≤ 2

Logo podemos afirmar que

R a i o   d o   O r i f í c i o → r = 1

R a i o   d a   E s f e r a → r = 2

Passo 3

Agora vamos resolver a nossa integral:

V = 2 ∫ 0 2 π ∫ 1 2 ∫ 0 4 - r ² r d z d r d θ

Começando pela mais interna:

∫ 0 4 - r ² r d z = r ∫ 0 4 - r ² d z

∫ 0 4 - r ² r d z = r z 0 4 - r ² = r 4 - r 2

Ficando agora

V = 2 ∫ 0 2 π ∫ 1 2 ∫ 0 4 - r ² r d z d r d θ = 2 ∫ 0 2 π ∫ 1 2 r 4 - r 2 d r d θ

Continuando na mesma ideia

∫ 1 2 r 4 - r 2 d r = - 1 3 ( 4 - r 2 ) 3 2 1 2

∫ 1 2 r 4 - r 2 d r = - 1 3 ( ( 4 - ( 2 ) 2 ) 3 2 - ( 4 - ( 1 ) 2 ) 3 2 )

∫ 1 2 r 4 - r 2 d r = - 1 3 0 - 3 3 2 = 3

Ficando agora

V = 2 ∫ 0 2 π ∫ 1 2 ∫ 0 4 - r ² r d z d r d θ = 2 ∫ 0 2 π 3 d θ = 2 3 ∫ 0 2 π d θ

Calculando a última integral:

2 3 ∫ 0 2 π d θ = 2 3 θ 0 2 π

V = 2 3 ∫ 0 2 π d θ = 4 π 3

Resposta

R a i o   d o   O r i f í c i o → r = 1

R a i o   d a   E s f e r a → r = 2

V = 4 π 3

Exercícios de Livros Relacionados

58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d