Uma cunha curva é obtida através de um corte perpendicular ao eixo de um cilindro, seguido de um corte que cruza o eixo formando um ângulo de , conforme a figura:
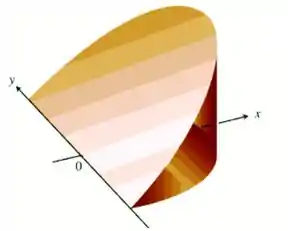
Sabendo que o cilindro possuía raio , antes de ser cortado, calcule o volume da cunha.
Passo 1
Bora lá. Como um bom primeiro passo, vamos pensar: como eu posso fatiar essa cunha de forma que as seções transversais tenham sempre o mesmo formato? Bem, uma boa ideia seria cortar ao longo do eixo . Saca só como fica:
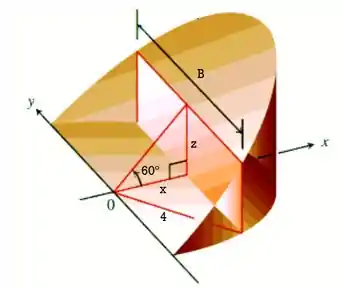
Opa, fazendo uma seção transversal perpendicular ao eixo eu achei um retângulo. E saca só, como em cada escolhido esse retângulo tem uma área diferente..
E se eu somar essas infinitas áreas eu acho o volume, logo:
Maravilha, mas antes de passarmos pro próximo passo, tem algumas simplificações que já conseguimos fazer. Veja só, o sólido está definido no eixo entre a origem e o raio! E a área do retângulo é a base vezes a altura! Show! Conseguimos reescrever o volume para:
Vamos modelar então e pra poder achar o volume, beleza?
Passo 2
Show de bola. Se olharmos beeem a figura, vamos ver que dois triângulos retângulos muito importantes aparecem. O primeiro é esse aqui ó:
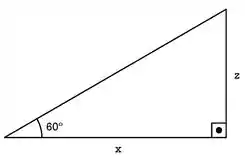
E esse triângulo tem tudo que precisamos pra achar ! Basta fazer a tangente do ângulo do corte! Vamos ter:
E o outro triângulo ta deitado lá de boas só olhando pra gente. Ele vai ser:
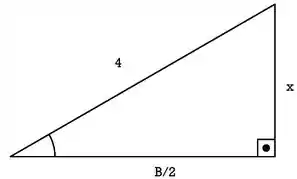
Pra esse que eu conheço todos os lados posso pedir ajuda pra Pitágoras, vamos ficar com:
E por fim:
E a integral fica:
Passo 3
Agora é só partir pras contas! Dada a integral:
Pra resolver eu posso olhar bem praquele ali pendurado e lembrar que se eu derivar um polinômio do segundo grau, eu acho um do primeiro! Então uma boa ideia é a substituição simples:
Como a integral é definida, vamos adaptar os limites de integração, beleza?
A integral vai ficar:
Finalizando: