USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista - Integrais Duplas e Teorema de Fubini, Questão 3
Determine o volume do sólido limitado pelas superfícies e para .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra calcular o volume do sólido limitado pelo cilindro e pelo plano , pra sempre positivo. No gráfico, esse sólido ficaria assim:
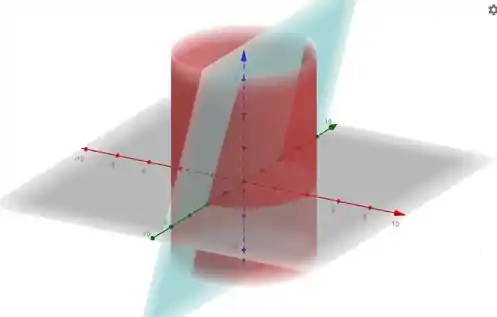
Como temos um cilindro e dois planos limitando a nossa região, vamos usar as coordenadas cilíndricas:
Assim, nós vamos descobrir os intervalos de integração e montar a nossa integral na forma:
Vamos lá!
Passo 2
Repare que pra , na figura, temos nosso ângulo variando de até . Logo,
O raio do cilindro varia conforme a equação . Então,
E o nosso varia verticalmente do plano até .Como , temos:
Prontinho, temos nossos intervalos. Vamos montar nossa integral:
Passo 3
Resolvendo primeiro para , temos:
Integrando agora em relação a :
Colocando a constante pra fora da integral:
E podemos integrar em relação a :
Aplicando os intervalos de integração:
E encontramos nosso volume.
Valeu, galera! Até a próxima! 😉