UFMG, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFMG - Lista 1 - Integrais Duplas e Triplas, Questão 19
Calcule a massa do sólido limitado pelo cone e pelo plano ; se a densidade de massa e dada por .
Passo 1
Eaee!!! Belezinha? Bom... queremos encontrar a massa do sólido limitado pelo cone e pelo plano , ou seja:
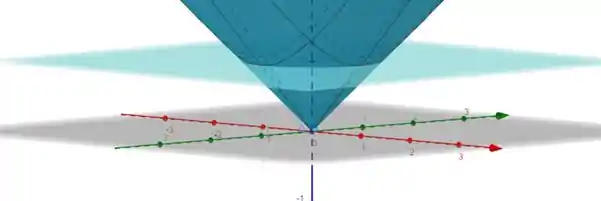
Lembrando que a densidade é dada pela divisão da massa pelo volume e que:
Para calcularmos a massa , temos que saber que:
Passo 2
Bom... em coordenadas cilíndricas, temos:
E que
Além disso, como a região de integração é circular, temos então que e .
E, para , temos:
Passo 3
Agora, integrando, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d