Encontre o volume do sólido cuja base é a região delimitada pelas curvas e cujas seções transversais perpendiculares ao eixo são quadrados
Passo 1
Bem, a gente não tem e nem vai ter a cara dessa figura, infelizmente, pra ajudar a gente. Mas relaxa gafanhoto, ainda da pra se safar. Pra começar, vamos enxergar a base da figura. Pra saber em quais valores de a região da base se fecha basta igualar:
E logo:
As soluções são então e . Show de bola. Como é uma parábola e uma reta, o gráfico da região que representa a base vai ser:
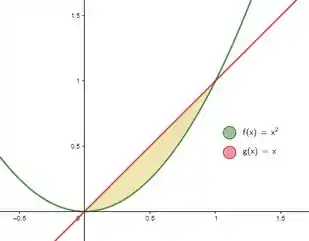
Passo 2
Ok, beleza, temos a base. Mas como isso nos ajuda? Bem, da uma olhada numa informação crucial do exemplo:
Se as seções transversais são perpendiculares ao eixo , no plano , podemos marcar algumas retas representando diferentes cortes transversais:
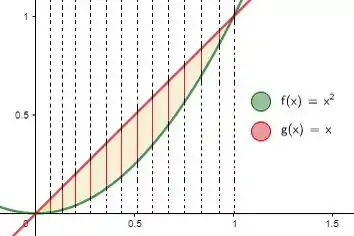
E olha só! Como essas sessões são quadradas essas linhas vermelhas não só são as bases do corte transversal, mas também a altura! Como cada linha vermelha tem o tamanho:
E como a área de um quadrado é:
Vamos ter:
Opa, show de bola, modelamos a área da seção transversal em função da posição de corte. Somando os infinitos quadrados que existem nesse sólido entre e , onde a base do sólido está definida, temos:
Passo 3
Pra fechar com chave de ouro, basta a gente resolver a integral: