UFRJ, Sem Campus, Cálculo 1, Listas Cálculo 1 - P2 - 2022.2, Questão 4
Encontre o volume obtido pela rotação em torno do eixo da curva: , . (Dica: Coloque em evidência)
Passo 1
Eaew, belezinha?
O enunciado nos dá a seguinte elipse
e queremos calcular o volume do sólido de revolução gerado ao rotacionar a elipse acima em torno do eixo . Temos que que como estamos considerando apenas a parte superior da elipse! A rotação forma o seguinte elipsóide
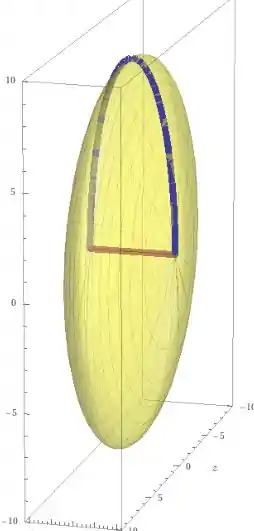
Para resolver vamos utilizar o método dos discos! Que se trata de calcular e somar a área de discos infinitesimais que descrevem o nosso sólido! Em nosso caso, temos discos cujo raio é dado pela função
em que usamos a dica do enunciado! Sendo assim, o método do disco se torna
em que os limites de integração são obtidos considerando um extremo da elipse até o outro no eixo ! Com tudo isso montado! Agora é só resolver! Vamos lá!!
Passo 2
Simplificando a expressão de nosso volume, temos que
Ambas integrais podem ser resolvidas usando que
em que temos para a primeira integral e a segunda , obtemos então que
Se avaliarmos os limites de integração, temos que
ou, simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!