Calcule o volume do sólido de revolução abaixo usando Cálculo de Volumes por Seções Transversais. O sólido foi feito girando a curva em torno do eixo .
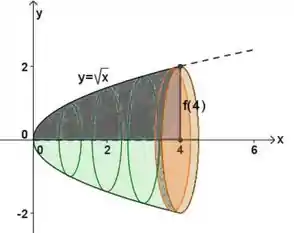
Passo 1
Vamos lá! Pra começar, a gente tem que usar o método de cálculo que aprendemos de Cálculo de Volumes por Seções Transversais. Pra isso, vamos lembrar do passo a passo dele:
- Escolher um eixo para fazer os cortes das seções transversais. Ex:
- Identificar a geometria da seção transversal e encontrar sua área. Ex:
- Relacionar variáveis da fórmula da área da seção transversal com o eixo escolhido. Ex:
- Encontrar sobre o eixo escolhido os valores no qual o sólido está definido, isto é, encontrar os limites de integração. Ex:
- Integrar:
E olha só! O nosso sólido já nos dá algumas dicas! O eixo mesmo tá cheio de círculos diferentes em alturas diferentes de ! Então vou escolher ele mesmo e a minha área vai ser a área de um círculo. Por enquanto temos:
Passo 2
Show, agora pra fazer o terceiro passo, vamos ter que arranjar um jeito de escrever como uma função de . Bem, na equação da área de um círculo , como é uma constante, não vai ter jeito. Escreveremos da seguinte forma:
Isso aiiiinda não diz muito pra gente pois não sabemos quem é . Mas relaxa gafanhoto, pq olhando novamente pra figura da pra pescarmos a ideia. Saca só:
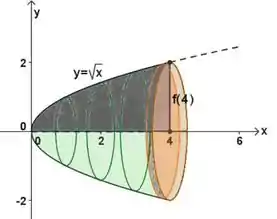
E saca só aquela fatia ali em . Pela figura conseguimos ver que o raio é a reta que sai do eixo e toca a curva , logo:
Então está feito! Se em temos o raio vai ter a seguinte fórmula:
E logo:
E ainda digo mais em! A imagem já mostra em que intervalos de o sólido está definido! Então fechamos o passo já que o sólido está definido entre e ao longo do eixo e modelamos finalmente a expressão do nosso volume:
Passo 3
Agora pra fechar com chave de ouro, só calcular o volume. Vamos ter: