Deduza o volume de uma esfera usando Cálculo de Volumes por Seções Transversais.
Passo 1
Partiu então. Pra começar, vamos das uma olhada na esfera num ambiente 3D:
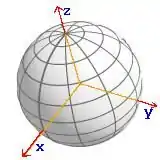
Beleza. Pela simetria então dessa esfera linda aí de cima, qualquer corte transversal perpendicular aos eixos resultará em um círculo. Se fizermos então perpendicular ao eixo vamos ter:
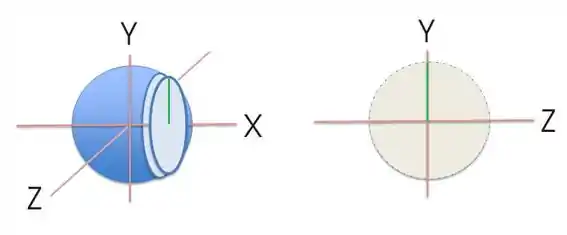
E somando as áreas dos infinitos círculos que podemos tirar com esse fatiamento, usamos a integral e achamos o volume da esfera:
Show, mas vamos modelar isso um pouco melhor. Veja, como a esfera está centrada na origem, em todos os eixos, ela está delimitada entre e . Pô, maravilha, então já sei os limites de integração:
E como todas as seções transversais são círculos a área deles vai ser:
E logo:
O que falta agora vai ser achar uma expressão pra essa integral ficar certinha e conseguirmos integrar. Bora lá então.
Passo 2
Agora pra pensar em como escrever o raio da seção transversal em função de , vamos olhar de novo pro corte que fizemos:
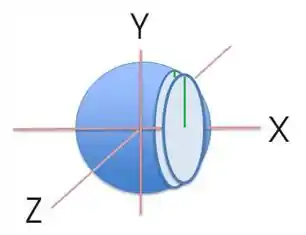
Note o seguinte, o raio do corte transversal lá de trás é maior que o corte transversal da frete! Só ver pela linha verde. Então de fato, a posição do corte determina o tamanho do raio. No plano podemos ver então os diferentes raios com diferentes tamanhos dependendo do corte:
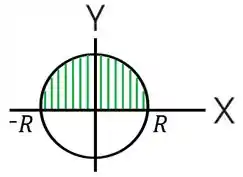
Mas olha que bacana: todos eles saem do eixo e tocam na circunferência! Isso quer dizer que o tamanho deles é:
Como a equação da circunferência é:
Isolamos o e ficamos com:
Como a integral era:
Modificamos ela pra:
E agora sim da pra integrar!
Passo 3
Integrando então:
O que finalmente, resulta em: