USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 2, Questão 5.11
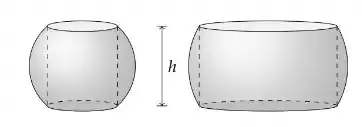
Um anel esférico é o sólido que permanece após a perfuração de um buraco cilíndrico através do centro de uma esfera sólida. Se a esfera tem raio R e o anel esférico tem altura h, prove o fato notável de que o volume do anel depende de h, mas não de R.
Passo 1
Para provar que o volume do anel esférico depende apenas da altura h e não do raio R da esfera, podemos utilizar uma abordagem geométrica e algébrica. Vamos começar dividindo o processo em duas etapas: uma esfera sólida completa e uma esfera menor, excluindo o anel.
Etapa 1: Esfera sólida completa
O volume de uma esfera é dado pela fórmula:
Etapa 2: Remoção do anel
Agora, vamos considerar a remoção de um cilindro da esfera, que resultará no anel esférico.
O raio desse cilindro é o raio R da esfera, e sua altura é h.
O volume do cilindro é dado por:
Passo 2
Quando removemos o cilindro da esfera, o que sobra é o anel esférico.
Portanto, o volume do anel é a diferença entre o volume da esfera completa e o volume do cilindro:
Agora, vamos simplificar essa expressão fatorando o termo em comum:
Passo 3
Neste ponto, podemos observar que o termo dentro dos parênteses não contém o raio R da esfera, ou seja, o volume do anel não depende de R.
Apenas depende da altura h do anel.
Portanto, concluímos que o volume do anel esférico depende apenas da altura h, mas não do raio R da esfera, como foi demonstrado.
Resposta
Vide o passo a passo.