Cálculo de Volumes através de Integrais
Considere a região plana delimitada pela curva , pelos eixos coordenados e pela reta . Calcule o volume do sólido gerado pela rotação dessa região em torno do eixo .
Passo 1
Repara, a região é limitada pelos eixos e , pela reta , que é uma paralela ao eixo que passa no ponto , e a função . O domínio dessa função pede , com o valor em sendo . Repara que não precisamos saber como é o desenho dessa curva, já que a integral não será afetada por seu desenho ou pelo esboço. Isso por que esse é o único gráfico que estudamos na questão e estamos girando no eixo , o que não gera nenhum tipo de problema, uma vez que o gráfico de será sempre maior que , já que:
Assim, fiz o meu esboço para uma curva qualquer do :
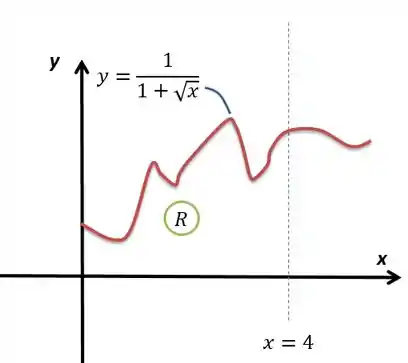
Inventei o meu próprio desenho para a curva, já que não vai mudar em nada na integral. :P
Passo 2
Giramos em torno do eixo , o que pede como melhor método o das seções transversais mesmo. Vendo isso, a integral que gera o volume pedido vai ser essa aqui, olha:
Essa integral não lembra nenhum método de integração de primeira, por isso vou tentar forçar uma substituição para mudar a cara dela:
Acontece que ali na questão nós não temos esse achado aqui em cima. Vamos forçar ele a aparecer então:
Já que . Substituindo na integral, ficamos assim:
Passo 3
Para a primeira integral, podemos dizer que , o que geraria exatamente um valendo .
Para a segunda, se chamarmos de uma variável teremos:
Passo 4
Fazendo agora a diferença entre os dois resultados:
Finalmente, esse é nosso volume!