UNB – Sem Campus – Cálculo 1 – Listas – Listas de Aplicações Calculo 1 – UNB – Questão 3
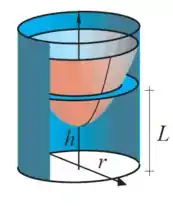
Considere um recipiente cilíndrico de raio , inicialmente em repouso com água até a altura . Em seguida, o recipiente começa a girar até que, juntamente com a água, alcance uma velocidade angular constante igual a . Nesse caso, a superfície da água corresponde à rotação, em torno do eixo , do gráfico de uma função , com . Não havendo perda de água, pode-se mostrar que , onde é a aceleração da gravidade e é uma constante que depende de .
O volume do sólido de rotação do gráfico de em torno do eixo é igual a Use essa informação para calcular o volume de água no recipiente em termos de e .
Usando o item anterior, obtenha como função .
Determine o valor de para que seja igual à metade da altura da água em repouso.
Passo 1
Oiie, tudo certinho contigo?
O enunciado nos descreve a situação física idealizada de um balde cilíndrico com um certo volume de água que é rotacionado. A água tende a subir pelas paredes, e nos é dado que este movimento é descrito pela função . A alternativa pede para calcularmos o sólido de revolução desta função utilizando a definição que nos foi dada, isso nos permite utilizar a conservação do volume de água para calcular a alternativa , e por fim, utilizar este resultado para obter a alternativa .
Vamos com calma que tudo dá certo! Vem comigo!
Passo 2
Vamos usar a definição dada na nossa alternativa para calcular o volume pedido, temos
Como temos que , podemos escrever
Que pode ser separado em duas integrais individuais, como
Precisamos resolver as integrais agora! Bora lá!
Passo 3
Podemos identificar as integrais como
Em que podemos avaliar os limites para obter
Analogamente, temos para a outra integral que
E, da mesma, forma
Podemos substituir ambas na equação (2)! Vem comigo!
Passo 4
O nosso volume toma a seguinte forma
Apenas rearranjando e simplificando termos, temos
Com este volume em mãos podemos partir para a nossa alternativa . Vamo que vamo!
Passo 5
Como não perdemos água durante a rotação, temos que o volume que obtemos na equação (3) deve ser igual ao volume inicial da água! Que como está estabelecido no enunciado, ocupava um cilindro de altura , e, portanto, um volume
Como o volume se conserva, temos
Dividindo ambos os lados por , obtemos que
E, portanto, a altura é tal que
Faltando só mais uma! Desanima não! Vamos lá!
Passo 6
Agora, nos é pedido para encontrar tal que , ou seja, a altura é metade da altura inicial da água. Usando a equação (4), temos que
Temos que isolar , portanto, primeiro vamos isolar o termo que tem , para obter
Isolando
E, assim, a intensidade da rotação é tal que
A questão é isso! Te vejo na próxima! Tchau Tchau!
Resposta