UFSC, Joinville, Cálculo II, Provas Profº Rómulo Castillo - P1 2015.1, Questão 2b
Formule a integral que calcula o volume do sólido obtido ao girar a região limitada pelas curvas , , e ao redor do eixo apontado:
b) ao redor do eixo
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume do sólido obtido ao girar a região de interseção das curvas ao redor do eixo . Como nossa região gira em torno de um eixo paralelo ao eixo , seu volume é dado pela equação:
O raio , nesse caso, é dado pelas funções e , assim:
Então, vamos lá montar nossa integral!
Passo 2
Para as curvas dadas, nossa região que vai rotacionar é essa aqui:
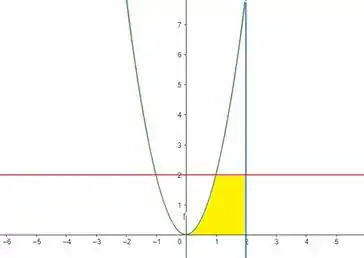
Como ela tá variando de a , temos:
Expandindo o produto:
Calculando a integral:
Aplicando os limites de integração, temos:
Logo,
Prontinho, galera! Até a próxima! 😉
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d