UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Integrais, Questão 11.4b
Seja R a região limitada pelos gráficos de e para e S o solido obtido pela revolução desta área em torno do eixo y.
- Calcule o volume de S.
Passo 1
Olá meu amigo, Yuri aqui, e agora vamos dar inicio a resolução dessa querida questão, onde iremos calcular o volume de revolução de uma função.
Antes de tudo, vamos dar uma olhada na região S.
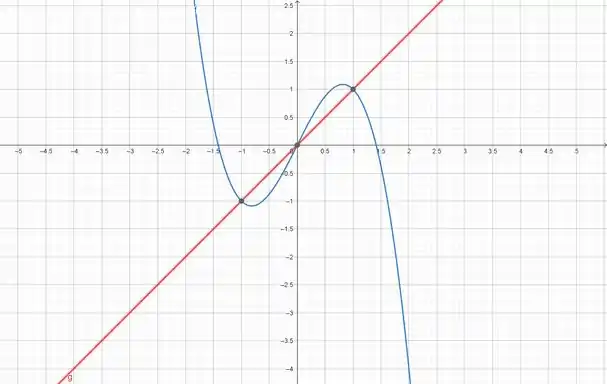
O volume do solido S é dado pela equação
Passo 2
Como temos uma simetria no nosso volume, poderemos calcular o da origem até e dobrar o valor encontrado.
A função é a mais externa, sendo ela a . Mas note que para facilitar nossas vidas, podemos girar esse solido em relação ao eixo x, pois aqui temos uma simetria
Resolvendo nossa querida integral, encontramos
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d