UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 3.4b
(4) Utilize o Teorema de Pappus-Guldin para determinar:
(b) o volume do sólido de revolução gerado pela rotação do triangulo com vértices nos pontos , , ao redor do eixo .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos que aplicar o teorema de Pappus-Guldin para determinar o volume do solido de revolução gerado pela rotação, através do eixo , do triangulo de vértices , , .
Tem ideia de como fazer isso? 🤔
O teorema de Pappus-Guldin nos diz que o volume de um solido de revolução é dado por
Onde é a distância do centroide da área a ser revolucionada e é sua área.
Primeiramente vamos obter o gráfico da área que vamos revolucionar, calcular sua área e a distância do seu centroide até o eixo de rotação.
Sacou? Bora começar! 😉
Passo 2
Vamos começar esboçando o triangulo e calculando seu centroide.
O centroide de um triangulo pode ser obtido a partir de seguimentos que ligam o vértice até o ponto médio do lado oposto a esse vértice. O cruzamento desses seguimentos para todos os vértices é o centroide no nosso triângulo.
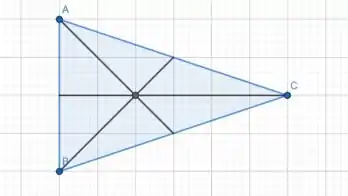
Perceba que o centroide está na metade da altura entre e e também em da altura entre e .
Portanto o centroide do triangulo é dado por
Dessa forma a distância do centroide até o eixo de rotação é dado por
E por fim, a área do triangulo é dado por
Onde é o comprimento da base e é o comprimento da altura.
Se considerarmos o seguimento como a base, vemos que e
Logo, a área do triangulo é dado por
Tranquilo até aqui? 😬
Passo 3
O que nos resta é substituir e na equação do teorema
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
