UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P1 2022.1, Questão 4
Seja a região limitada verticalmente por e , e lateralmente por . Esboce a região e calcule seu volume.
Passo 1
Oiie, tudo bem com você?
O enunciado apresenta uma região que tem algumas limitações, primeiro, ela é limitada pelo plano e a esfera , note que ele usou coordenadas cilíndricas para escrever esta expressão. A região também é limitada lateralmente pela superfície
que é um cilindro! Vamos fazer um esboço da região, e então calcular o volume dela, ou seja, resolver a integral tripla
em que o principal desafio é obter os limites de integração! Bora lá!
Passo 2
Vamos reescrever a expressão
se passarmos para o lado esquerdo e completar o quadrado somando e subtraindo , temos que
ou simplesmente
que é a equação de um cilindro em coordenadas cilíndricas de raio , mas com centro . A região é a seguinte
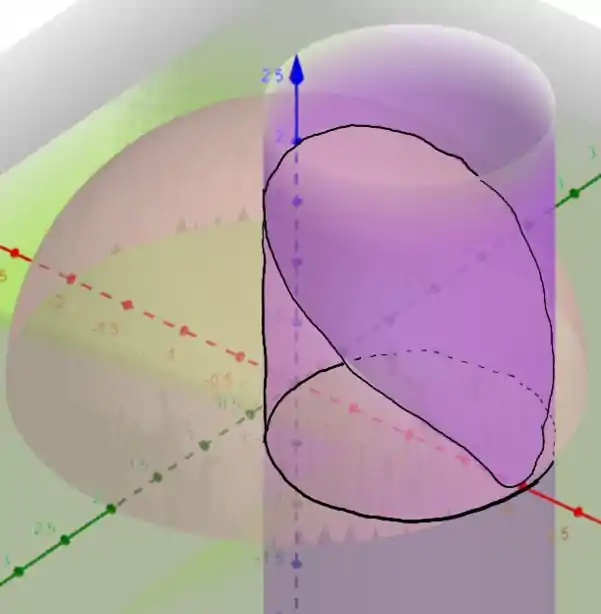
Vamos escrever a nossa integral de volume agora!
Passo 3
Note que nosso cilindro está fora do centro do sistema de coordenadas, portanto, vamos ter que tomar um pouco de cuidado na hora de estabelecer nossos limites de integração. Em coordenadas cilíndricas
e
o elemento de volume será . E, as superfícies tomam a forma
e
então, temos que a coordenada radial que descrever a nossa esfera em coordenadas cilíndricas, nos leva de até que é o nosso cilindro. E, também, como temos que a superfície não está simétrica em relação ao eixo , o ângulo se inicia em e vai até para descrever completamente a nossa região, sendo assim, nossa integral se torna
Vamos começar a integrar! Bora lá!
Passo 4
A integral em é bastante simples, temos que
de forma, que nosso volume se torna
para resolver a integral em , vamos fazer a substituição simples
e
de forma que podemos escrever
usando que
e voltando as variáveis originais , temos que
ou, usando que , temos que
Uff… Vamos para a última integral agora!
Passo 5
Usando o resultado do último passo temos que
a primeira integral é um pouco mais simples, temos que
Para a outra é conveniente reescrever um pouco nosso integrando como
e, como temos que , podemos escrever que
A primeira integral é conhecida como
ou simplesmente
Agora, para a outra integral, iremos precisar fazer a substituição simples
e
de forma que
usando que e , temos que
Finalmente, a nossa integral se torna
Finalmente, o volume será simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!