Encontre o volume do sólido cuja base é a região parabólica
e cujas seções transversais perpendiculares ao eixo são quadradas.
Passo 1
Olha, a princípio essa questão parece meio doida visto que a única real informação é a região da base. Vamos começar trabalhando então com ela e depois interpretamos o resto, belê? Saca só, do enunciado e de , podemos tirar:
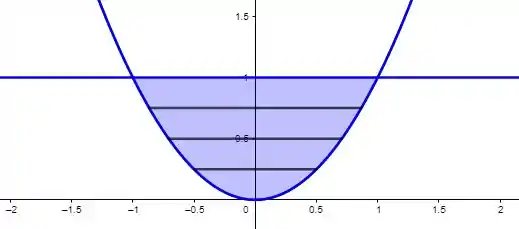
Agora temos como ver melhor o esboço. A região está de alguma forma delimitada pela parábola e pela constante . No gráfico, isso fica:
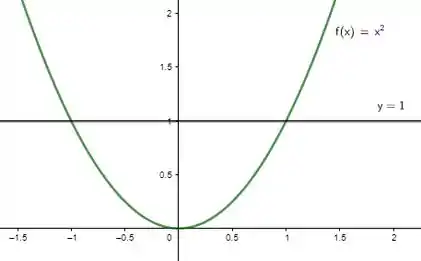
Como a região que eu quero é a abaixo da constante e acima da curva, vamos ter a interseção entre as duas regiões:
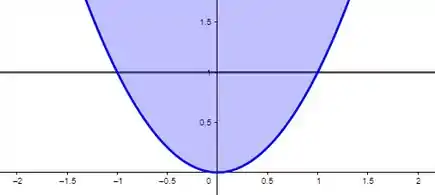
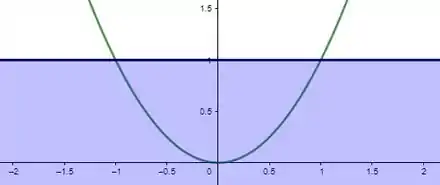
O que dá:
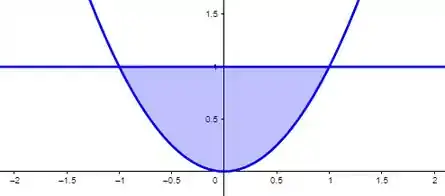
Show, entendemos a região da base. Segura essa informação na cachola que vamos precisar dela nos próximos passos.
Passo 2
Agora a gente parte pra interpretação de texto. Olha o que o enunciado disse:
Então pra entender bem, vamos fazer vários cortes perpendiculares ao eixo em :
E saca só! Pra cada corte , o comprimento do segmento marcado vai ser do até o correspondente aquela altura de corte . Veja por exemplo o corte em . Como temos:
Agora vamos colocar isso em função de uma vez que os cortes estão feitos ao longo desse eixo:
Ok, mas e daí? Onde que isso nos leva!? Oras meus caros! Esse comprimento que calculamos nada mais é do que o lado de um quadrado! Isso porque as seções transversais, segundo o enunciado, são quadradas. Como conhecemos áreas de quadrados, a área da seção transversal vai ser então:
Maravilha, então conseguimos modelar. E sabemos os limites de integração também porque eles são os valores de que fecham a região da base do sólido: o limite inferior e o limite superior . Da formulinha de volume por seções traversais, temos: