IME, Cálculo 1, 2020, VF, Q2A
Seja a área o conjunto de pontos tais que , , e .
- Determine o volume gerado pela revolução da área em torno da reta ;
- Determine o volume gerado pela revolução da área em torno da reta .
Passo 1
Molecada boa, vambora! Antes de tudo precisamos desenhar nossa região. Visto que as parábolas tem eixo de simetria no eixo fica mais simples, mas no final obtemos:
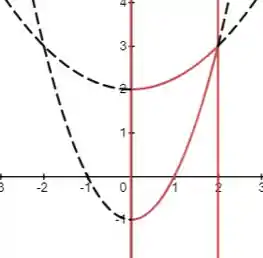
A fim de calcular o volume de revolução em torno de , utilizaremos cascas cilíndricas de raio e altura , com espessura , o volume pelas cascas seria:
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d