Provas antigas – Cálculo 2 – Unicamp – P2 6ª noite – questão 3
Determine o volume da região E limitada pelos cilindros e pelos cones ,
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?]
O problema nos pede para calcularmos o volume. Como é esse volume?
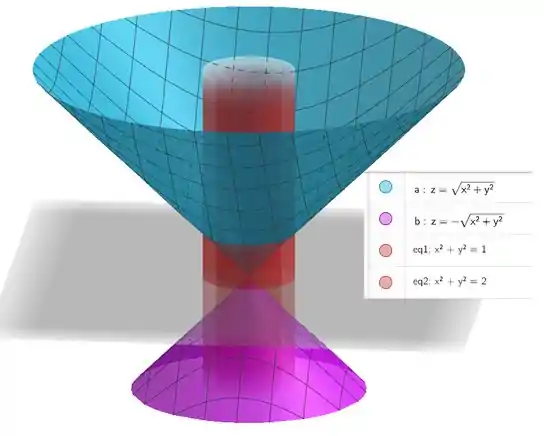
E bom, Mogli... Como eu resolvo esse abacaxi?
Primeiramente, sabemos que a integral de volume é dada por:
Isso em coordenadas cartesianas, mas claro que isso pode variar de acordo com a simetria do objeto/volume. E também a ordem de integração pode mudar, poderia ser por exemplo ou outras combinações
O Lance aqui é: Qual a melhor maneira de olhar, ou melhor, qual o melhor ponto de vista para interpretarmos esse problema?
Um outro ponto de vista pode nos ajudar a resolver o mesmo problema por diferentes formas
E bom... veja que aqui nós temos um problema que envolve objetos cilíndricos. O que é melhor para descrevê-los do que as próprias coordenadas cilíndricas?
E com isto, é por elas que vamos resolver esse problema, com as coordenadas cilíndricas!!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo assim, nós temos:
E ainda, as coordenadas cilíndricas são:
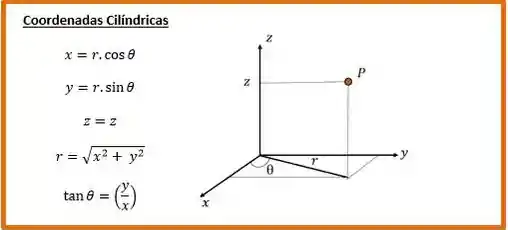
Agora basta-nos olhar para o mesmo objeto e ver como que são essas coordenadas.
Passo 3
Então vamos lá, vemos que:
Mas temos pelas coordenadas cilíndricas que:
Assim:
Mas Mogli, se é não deveríamos ter ? Não! Lembra que é o modulo da distância do raio, nesse caso não tem como
Também vemos que:
Mas de novo , logo:
E por fim, temos que é o ângulo de giro. Por ser um círculo completo no cilindro, vemos que:
Resumindo tudo que fizemos aqui:
Mas a vida seria muito doce se pudéssemos apenas trocar o ponto de vista de objeto assim facilmente. Infelizmente não é! Existe um termo de compensação chamado de Jacobiano. Sempre que voc�� realizar uma troca de coordenadas precisa saber como que esse termo de compensação é nessa coordenada.
Para o caso das coordenadas cilíndricas:
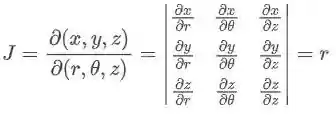
E agora sim, temos tudo que precisamos pra nossa integral!
Passo 4
Sendo assim:
Como é a variável de integração ? É ? É ? Veja que no nosso caso nada depende de , logo a sua ordem de integração não nos interessa, pode estar onde bem quisermos. Mas para não, veja que ele depende de , assim ele deve vir antes de , podemos fazer por exemplo .
Integrando em temos:
Integrando em :
Veja que é constante para . Assim:
E prontinho, resolvemos a nossa questão.
Resumindo:
Sendo :
Resposta
Sendo V: