UFSC, Araranguá, Cálculo B, P3 - 2022.2, Questão 2
Determine o volume do sólido delimitado pelas superfícies e .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu duas superfícies (dois paraboloides) e pediu pra gente calcular o volume entre elas. Vamos dá uma olhada em como são essas superfícies:
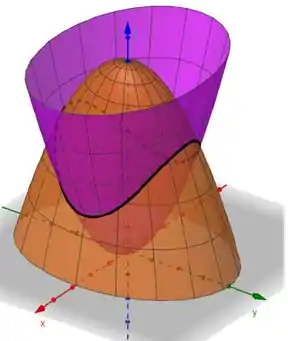
Pra calcular o volume entre essas duas superfícies, nós vamos igualar as duas equações que o enunciado nos deu, pra encontrar o raio da projeção da figura no plano . Em seguida, nós vamos definir a função de integração e seus intervalos, pra, assim, calcular o volume.
Vamos lá!
Passo 2
Vamos começar igualando as equações e :
Colocando em evidência:
Lembra que em coordenadas polares, ? Então, vamos substituir na equação:
Então nosso varia de até o raio . Repare que a equação que nós encontramos igualando as equações, nos dá uma circunferência. Então, nosso ângulo vai variar de até . Resumindo tudo isso, fica assim:
Passo 3
Agora vamos determinar nossa função a ser integrada. Olhando para o nosso gráfico do passo , nós vemos que a nossa superfície pode ser obtida fazendo:
Resolvendo, temos:
Mas a gente precisa que a nossa função tenha a forma . Então, vamos usar de novo a relação . Substituindo, temos:
Essa é a nossa função de integração.
Passo 4
Agora podemos montar nossa integral pra calcular o volume :
Vamos integrar primeiro em relação a :
Aplicando os intervalos de integração em :
Agora nós podemos colocar a constante fora da integral e integrar em relação a :
Aplicando os intervalos de integração em :
E encontramos nosso volume.
Valeu, galera! 😉