UFMG, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFMG - Lista 1 - Integrais Duplas e Triplas, Questão 21
Calcule o volume do sólido .
Passo 1
Eaee!!! Belezinha? Bom... queremos encontrar o volume do sólido .
De forma gráfica queremos encontrar o volume do seguinte sólido:
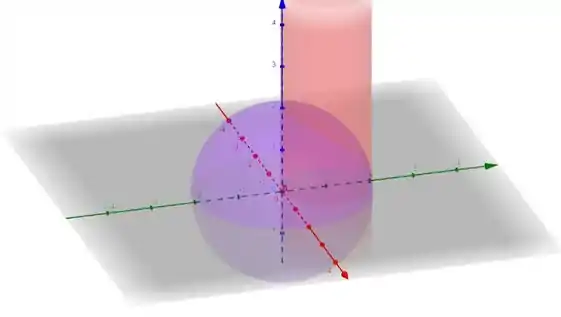
Seja .
Essa integral pode ser calculada a partir da subtração de outras duas, sendo elas a integral tripla sob a circunferência em coordenadas esféricas e a integral sob o cilindro nas mesmas coordenadas.
Passo 2
Bom... dessa forma, temos:
- Na esfera:
- No cilindro:
Obs: nos dois casos, consideramos metade do intervalo e multiplicaremos por .
Passo 3
Agora, integrando, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d