UERJ, Sem Campus, Cálculo II, Provas de Cálculo 2 - Profº Filipe Iorio - 1ª Prova, Questão 1
1) Seja . Classifique e esboce as curvas de nível . Para quais valores de temos que a curva de nível correspondente é não vazia? Esboce o gráfico de .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos que obter as curvas de níveis da função , obter os valores de que as curvas que não são vazias e esboçar o gráfico de .
E aí, como resolvemos esse problema? 🤔
Para obter as curvas de níveis de uma função, igualamos a função a uma constante e que cada valor de corresponde a um nível de , ou seja, uma altura do plano .
Sacou? Bora ver como fazemos isso. 👀
Passo 2
Igualando a , temos
Manipulando essa equação, temos
Perceba que essa equação que encontramos, é muito parecido com a equação da circunferência dada genericamente por
Onde e são as coordenadas do centro da circunferência e é o raio da circunferência.
Entendeu essa parte? 😉
Passo 3
Para , temos que ter sempre um valor maior que , já que raio negativo não existe. Ou seja, o termo tem que ser maior que ...
Como está ao quadrado, temos que tirar a raiz nos dois lados e quando fazemos isso em uma inequação, temos que aplicar em um intervalo, pois pode ser positivo ou negativo.
Portanto, os níveis não vazios de são os níveis entre e
Tranquilo até aqui? 😁
Passo 4
Agora vamos esboçar as curvas de níveis de para , e .
Para , temos
Ou seja, uma circunferência centrada em e com raio .
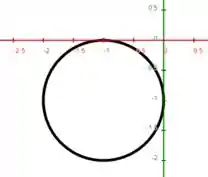
Agora para ...
Agora outra circunferência com centro em e com raio
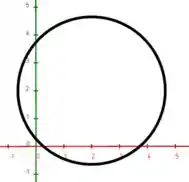
E por fim, para , vamos substituir na primeira igualdade de
Portanto, em , temos uma reta dada por
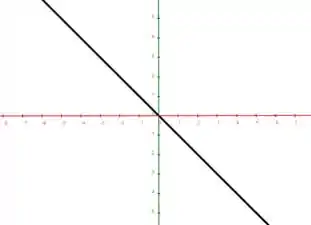
Interessante, não é? 😎
Passo 5
E finalmente, para obter o gráfico de vamos usar o que sabemos das curvas de níveis.
Perceba que quanto mais próximo de , maior é o raio da curva de nível e se for negativo, a circunferência é centrada no terceiro quadrante, já se for positivo, a circunferência é centrada no primeiro quadrante.
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
