USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 9c
9. Em cada item, esboce no mesmo plano coordenado as curvas de nível para :
(c)
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema queremos as curvas de nível da função nos níveis .
Lembra como fazemos isso? 🤔
O que temos que fazer é igualar a função a uma variavel que representa o nível da função que temos que representar...
Assim temos que atribuir a os valores e em cada equação formada, vamos ter um gráfico bidimensional que vamos ter que representar no plano cartesiano.
Sacou? Bora ver como é na prática! 😉
Passo 2
Igualando a função a , temos
Simplificando a equação...
Perceba que a equação resultante é muito parecida com a equação da circunferência, não é?
Onde é o centro da circunferência e é o raio...
Trazendo isso para o nosso caso, vamos obter que o centro das nossas curvas serão em e terão raio .
Por exemplo para ...
Para
E para
Representando essas equações no plano cartesiano, vamos obter
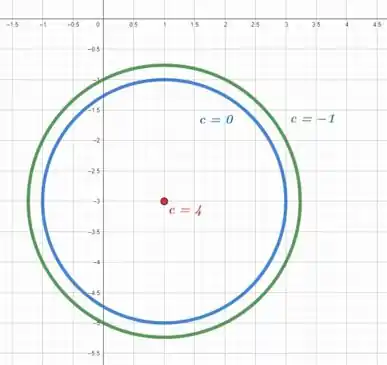
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
